Quantum field theory predicts that the temperature of empty space should depend on the observer’s motion, increasing proportionally with acceleration. Here I attempt an accessible introduction to this striking effect, related to Hawking radiation and discovered independently by Fulling, Davies, and Unruh, assuming only sophomore-level physics (including hyperbolic functions) with some assistance from Mathematica.
Hyperbolic Motion
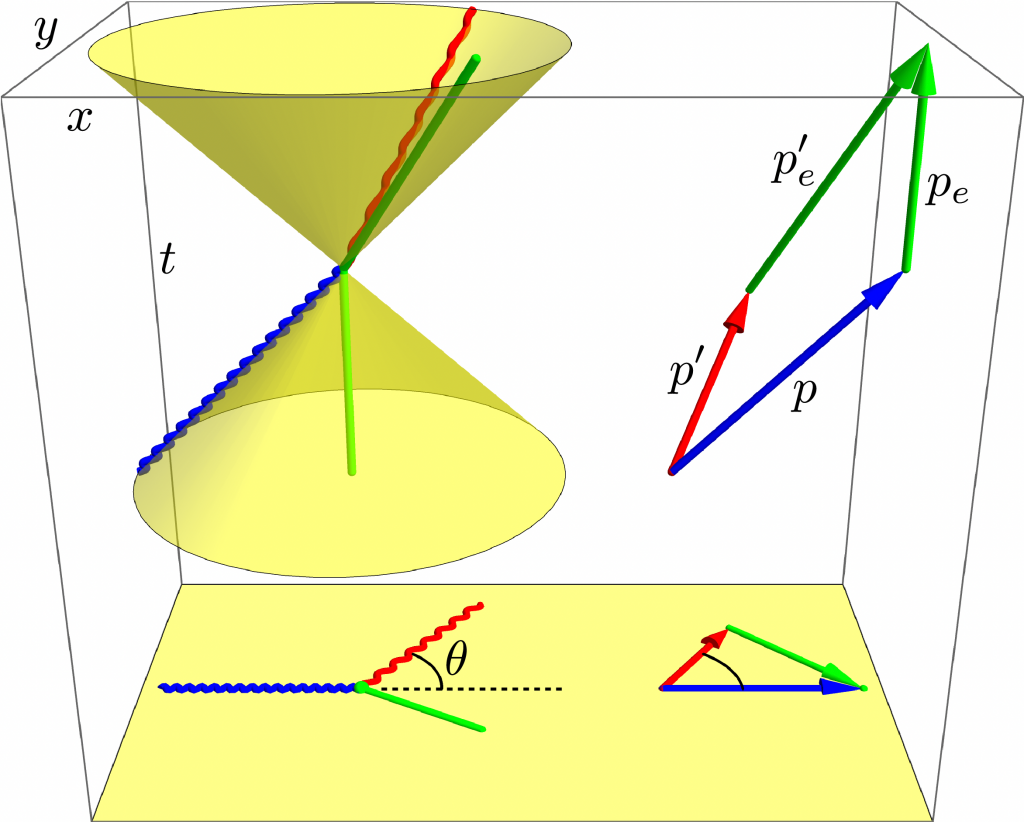
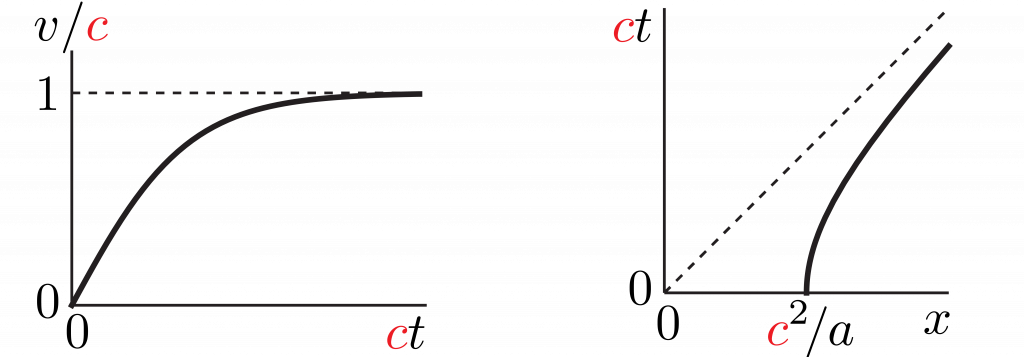
Constant acceleration in Newtonian mechanics is parabolic, while constant acceleration in Einsteinian mechanics is hyperbolic and asymptotic to light speed c = 1 in natural units. For 1+1-dimensional Minkowski spacetime, the difference in squared space and time displacements is the square of proper time displacement,
d\tau^2 = dt^2 - dx^2.
For constant proper acceleration, this has the solution
dt = d\tau \cosh a\tau,vdx = d\tau \sinh a\tau,
with velocity
v = \frac{dx}{dt} = \tanh a\tau \le 1,
where for small times v \sim a \tau \sim a t. If t = 0 and a x = 1 at \tau = 0, then integration gives
a t = \sinh a \tau,\\a x = \cosh a\tau.
Hyperbolic identities then imply
a^2 x^2 - a^2 t^2 = 1
and
a x + a t = e^{a\tau}.
Quantum Vacuum
Due to Heisenberg indeterminacy, electromagnetic fluctuations fill the vacuum. Consider a single such sinusoidal wave of angular frequency \omega_0 = k_0 in natural units. If you move at constant velocity, you observe the wave doppler-shifted to a different frequency. But if you move at constant acceleration, you observe the wave doppler-shifted to a range of frequencies corresponding to your range of velocities. For an accelerated observer at time \tau,
\phi[x,t] = \exp\left[i(k_0 x + \omega_0 t)\right] = \exp\left[i\omega_0(x + t)\right] \\= \exp\left[{i \frac{\omega_0}{a} e^{a \tau}} \right] = \phi[\tau].

Expand this waveform as a sum of harmonics
\phi[\tau] = \int_{-\infty}^{\infty}\,\frac{d\omega}{2\pi} \Phi[\omega] \exp[-i \omega \tau]
where the Fourier components
\Phi[\omega] = \int_{-\infty}^{\infty}d\tau\, \phi[\tau] \exp[+i \omega \tau].
To regularize this divergent integral, subtract a tiny imaginary part i \epsilon from the angular frequency \omega to incorporate a decaying exponential factor e^{-\epsilon \tau} in the integrand, and zero it after integrating. Find
\Phi[\omega] = \lim_{\epsilon\rightarrow 0} \int_{-\infty}^{\infty}d\tau\, \exp\left[ i \frac{\omega_0}{a} e^{a\tau} \right] \exp[+i (\omega - i \epsilon) \tau]\\~ \\= \lim_{\epsilon\rightarrow 0}\, \exp\left[ i\frac{\pi}{2} \left(\frac{\epsilon + i\omega}{a}\right) \right]\left(\frac{a}{\omega_0}\right)^{(\epsilon + i \omega)/a}\frac{1}{a} \Gamma\left[\frac{\epsilon + i \omega}{a} \right] \\= \exp\left[-\frac{\pi}{2} \frac{\omega}{a}\right]\left(\frac{a}{\omega_0}\right)^{i \omega / a}\frac{1}{a} \Gamma\left[i \frac{\omega}{a} \right],
where \Gamma[n+1] = n! analytically continues the factorial function to the complex plane. The spectrum is the absolute square of the Fourier transform,
S[\omega] = \left|\Phi[\omega]\right|^2 = \frac{\pi}{a\omega} \left(\coth\left[ \pi \frac{\omega}{a} \right]-1 \right) \\= \frac{2\pi}{\omega a} \frac{1}{e^{2\pi \omega/a} - 1} \propto \frac{1}{e^{\hbar \omega/k T}-1},
where the Planck factor suggests Bose-Einstein statistics and a thermal photon bath of temperature kT = a \hbar / 2\pi. In SI units,
T = \frac{a \hbar}{2\pi k c} \sim 40~\text{zK}~\left(\frac{a}{g_E} \right),
where g_E is Earth’s surface gravity, and a zeptokelvin is very cool.

Hawking-Unruh Temperature
Just prior to the 1970s work of Fulling, Davies, and Unruh, Stephen Hawking famously predicted that despite their reputations black holes should radiate with an effective temperature
T = \frac{\kappa \hbar}{2\pi k c},
where \kappa is the black hole’s surface gravity (observed at infinity). The Unruh and Hawking results may be linked by the equivalence principle, which equates acceleration and gravity, and by event horizons. In General Relativity, the black hole horizon is a boundary that causally disconnects the interior from the exterior. Similarly, when you accelerate, a Rindler horizon appears a distance c^2/a \sim 1~\text{ly} \left(g_E / a \right) behind you, causally disconnecting you from a region of spacetime whose photons you can outrun (so long as your acceleration continues).