Neural network does quantum mechanics

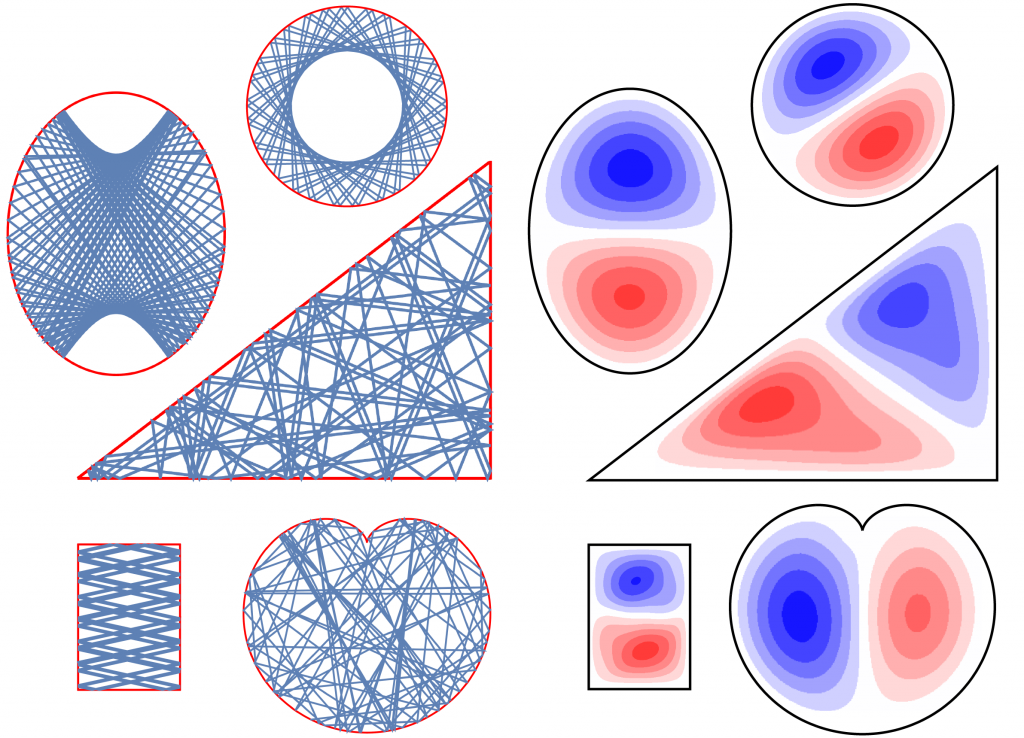
A particle confined to an impassable box is a paradigmatic and exactly solvable one-dimensional quantum system modeled by an infinite square well potential. Working with Bill Ditto, Elliott Holliday and I recently explored some of its infinitely many generalizations to two dimensions, including particles confined to regions that exhibit integrable, ergodic, or chaotic classical billiard dynamics, using physics-informed neural networks. In particular, we generalized an unsupervised learning algorithm to find the particles’ eigenvalues and eigenfunctions, even in cases where the eigenvalues are degenerate. During training, the neural network adjusts its weights and biases, one of which is the energy eigenvalue, so that its output approximately solves the stationary Schrödinger equation with normalized and mutually orthogonal eigenfunctions.