Thousands of years ago, ancient astronomers like Aristarchus and Eratosthenes combined careful observations with simple mathematics to measure the solar system, especially the diameters D of Earth, Luna (Earth’s moon), Sol (Earth’s star, the sun), and the radii r of their orbits. You too can do this, but it helps to observe an eclipse or two.
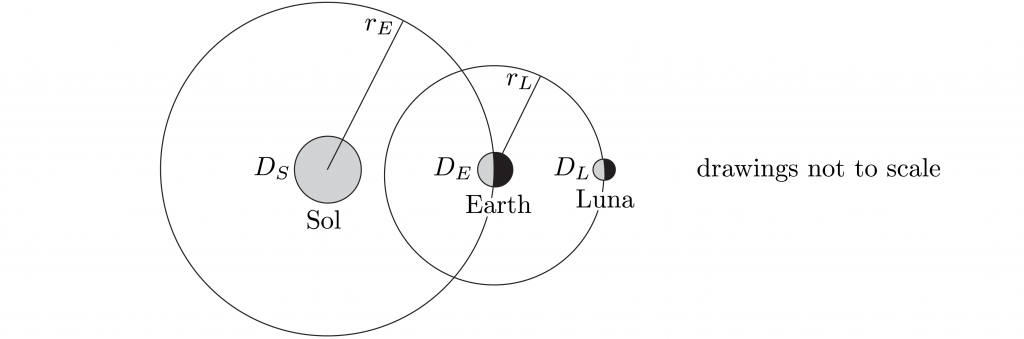
Step 1: Diameter of Earth
Measure how shadow lengths vary with latitude. No need to pace the distance between Alexandria and Syene, just use your favorite map software! Assume Sol is far from Earth (and check in Step 3), so Sol’s rays are nearly parallel.
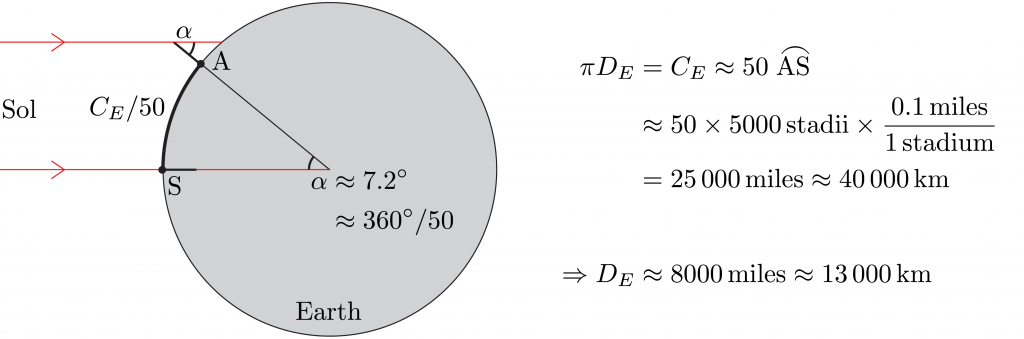
Step 2: Distance to Luna
Measure the duration of a lunar eclipse.
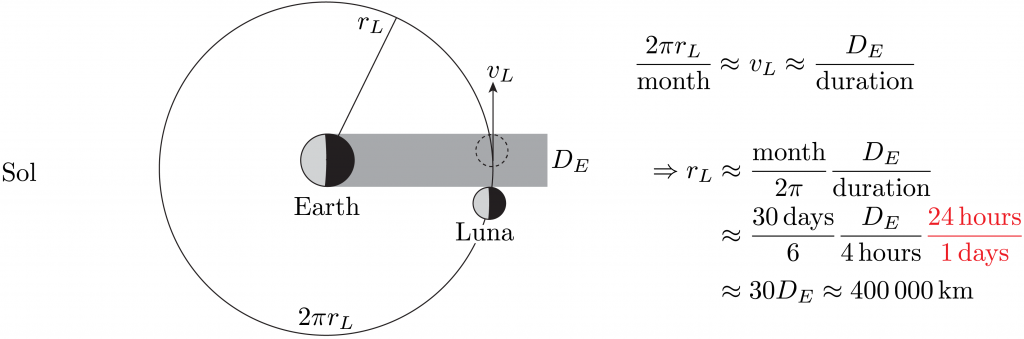
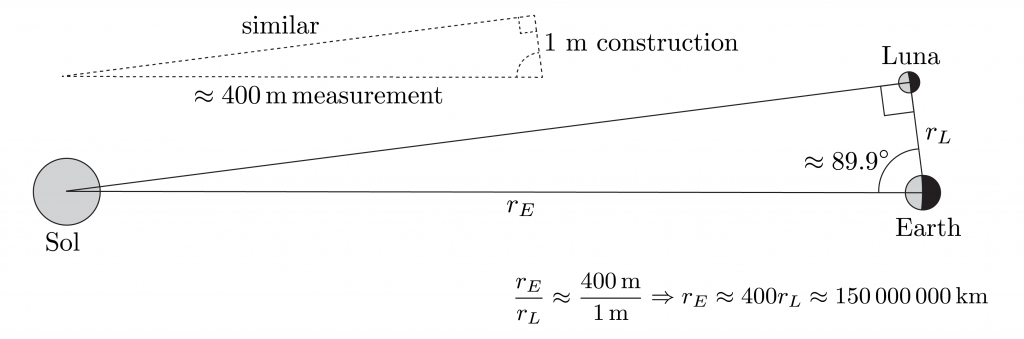
Step 3: Distance to Sol
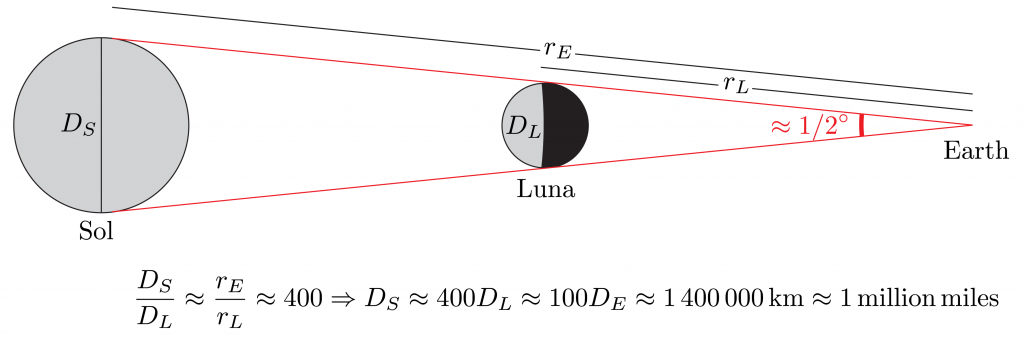
Measure the angle between Sol and Luna at first quarter moon, when Luna appears to be ahead of Earth in its orbit, like a signpost to a car on a road. This is the most difficult step, as the angle is nearly but not quite ninety degrees, but the result is the astronomical unit. (Alternately, measure the ratio of time Luna is crescent to gibbous.)
Step 4: Diameter of Luna
Measure the time for Luna to enter Earth’s shadow during a lunar eclipse. Consistent with Step 3, again assume Earth is far from Sol, so Earth’s shadow is nearly uniform.
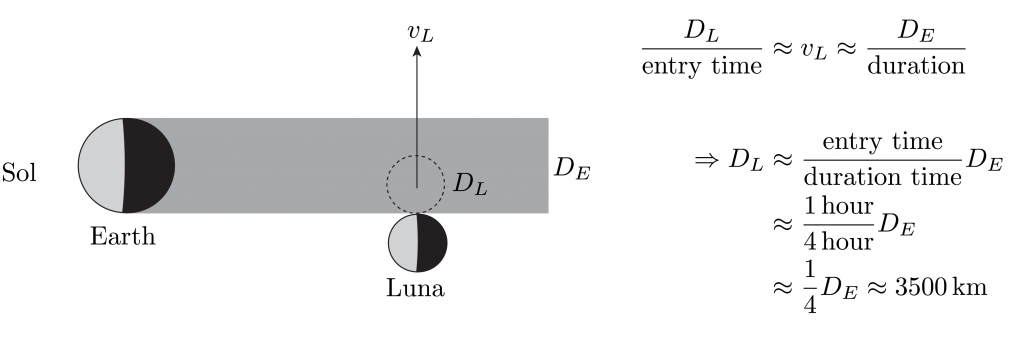
Step 5: Diameter of Sol
Note that Sol and Luna have about the same apparent angular size (both subtending about half a degree). This is most spectacularly evident during a solar eclipse, where Luna just barely covers Sol — if you were ever fortunate enough to experience a solar eclipse.
