Just a couple of months after announcing the remarkable discovery of a single shape that forces a non-periodic tiling of the plane, Smith, Myers, Kaplan, and Goodman-Strauss have announced an improved aperiodic monotile or ein stein. (Ein stein is “one stone” in German.)
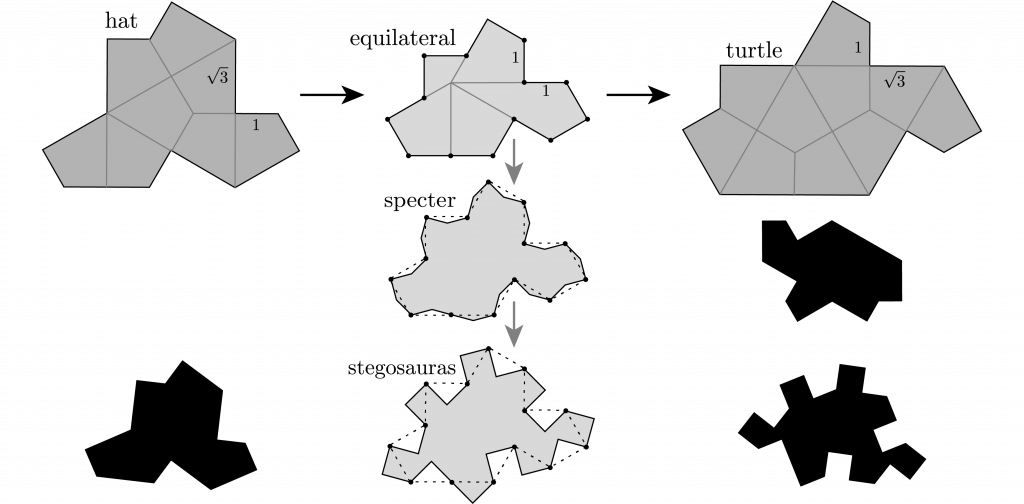
The hat and turtle shapes tile the plane only non-periodically, but with their mirror reflections, which would be practically troublesome for one-sided tiles. Smith and colleagues realized that if reflections are forbidden an intermediate equilateral shape tiles the plane only non-periodically. Furthermore, perturbing the shape’s sides can block periodic tiling using it and its reflection, thereby generating specter shapes that tile the plane only non-periodically, whether reflections are allowed or forbidden.
Because specters don’t need their reflections, and vampires are said to not reflect in mirrors, the authors playfully suggest calling them vampire ein steins. You could tile your bathroom with a single specter shape, even though bathroom tile is glazed on only one side!
Below are three different colorings of a tiling by a stegosaurus shape, a particularly simple equilateral specter with only \pm 60^\circ and \pm 90^\circ turns (and a single 0^\circ turn), which I created in Mathematica and Illustrator. The darker tile pairs in the first coloring are called mystics