The motion of one of the simplest dynamical systems, a torqued, damped, nonlinear pendulum, can be infinitely complicated.
Consider a simple pendulum of length l and mass m rigidly connected to an axle of radius r wrapped by a rope that hangs down one side with a mass M climbing up and down it, as in the attached animation.
If the climber’s height
x = x_0 + \frac{a}{\omega^2} \sin \omega t,varies sinusoidally (relative to the axle), then its acceleration
\ddot x = – a \sin \omega t,also varies sinusoidally, so the total force on the climber
M\ddot x = \sum_\text{down} f = Mg-Timplies upper rope tension
T = Mg + ma \sin \omega t,where 0 < a < g. If the axle and rope have negligible inertia, then the total torque on the axle
m l^2 \ddot \theta = \sum_\text{CCW}\tau = – mgl \sin\theta + rT – \gamma \dot\theta,where \gamma is the axle viscosity. The full motion equation
m l^2 \ddot \theta = – mgl \sin\theta + rMg + rma \sin \omega t – \gamma \dot\thetareduces to
\ddot \theta = – \sin\theta + 0.7155 + 0.4 \sin 0.25 t – 0.75 \dot\thetafor parameters that describe the animation’s chaotic motion.
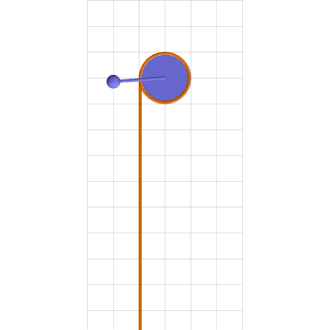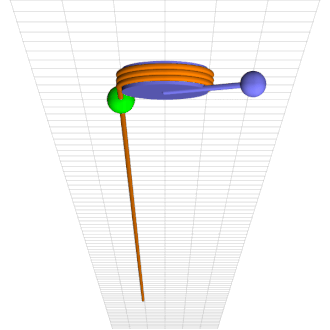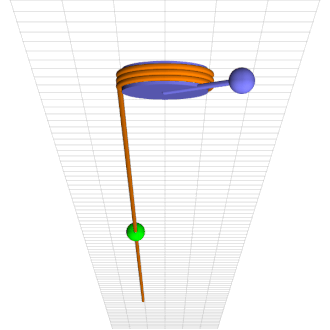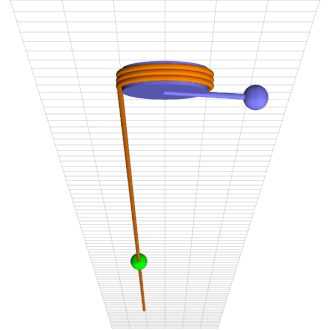

Thanks, Mark! I enjoy reading your posts as well.