After MANY months of not traveling, I scheduled a meeting with Robert (Bob) M. Mazo, Professor emeritus from the University of Oregon, now living outside Philadelphia.
In 1971/1972 he helped developing the key model to describe chemical reaction-diffusion systems. But, as he stated, he was “only the catalyst” and only accepted to be recognized in the acknowledgments. The now called FKN mechanics, named after the three authors Dick Field, Endre Kőrös, and Dick Noyes, was the first model to describe the necessary reactions to create temporal, spatial, and spatiotemporal patterns in the nonlinear chemical Belousov-Zhabotinsky reaction. It had been published between 1972 and 1974 in a series called Oscillations in chemical systems I, II, III, IV, and V.
I am honored to write a manuscript with him, now at age 91, and the sole survivor of the original FKN papers, Dick Field, for a special edition in Chaos this year to celebrate Dick Field’s 80th birthday last October. During our meeting, Dick Field joined us via Skype from Missoula, Montana. It was a wonderful time travel back five decades while they were exchanging anecdotes and talked about nearly forgotten stories.
At the end of our meeting he joked that people in 50 years will know pretty much exactly which year our selfie had been taken…


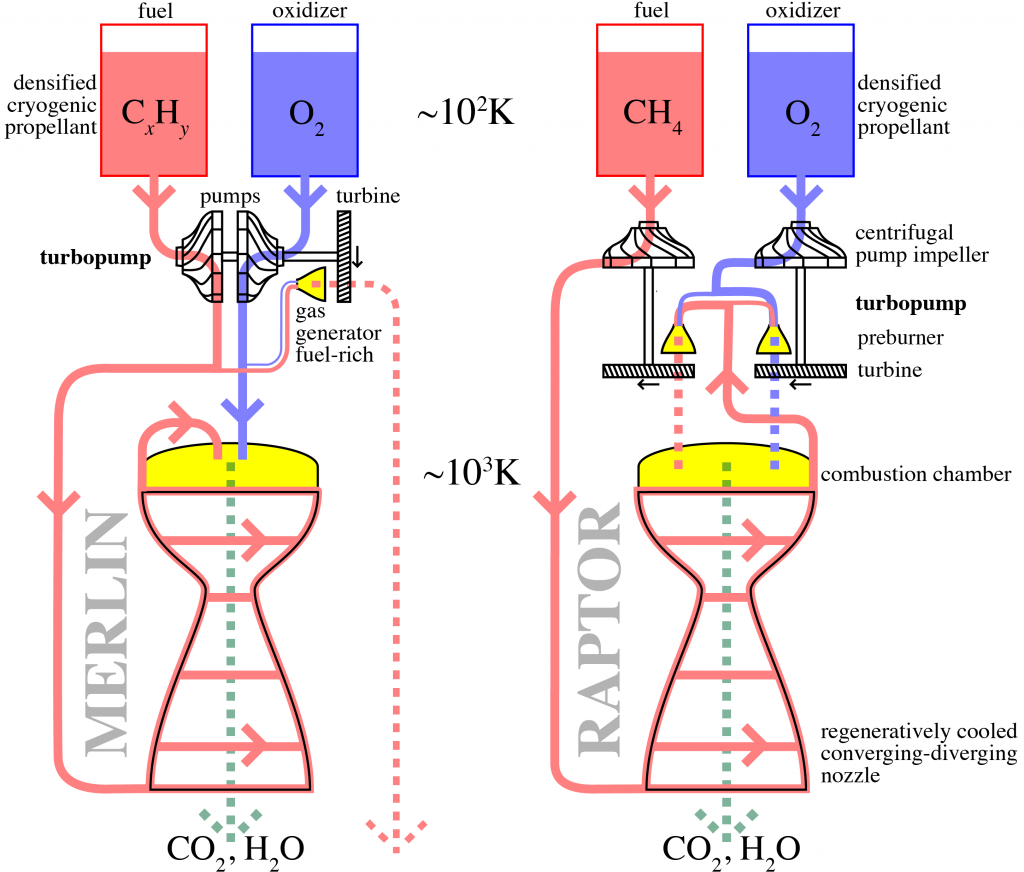
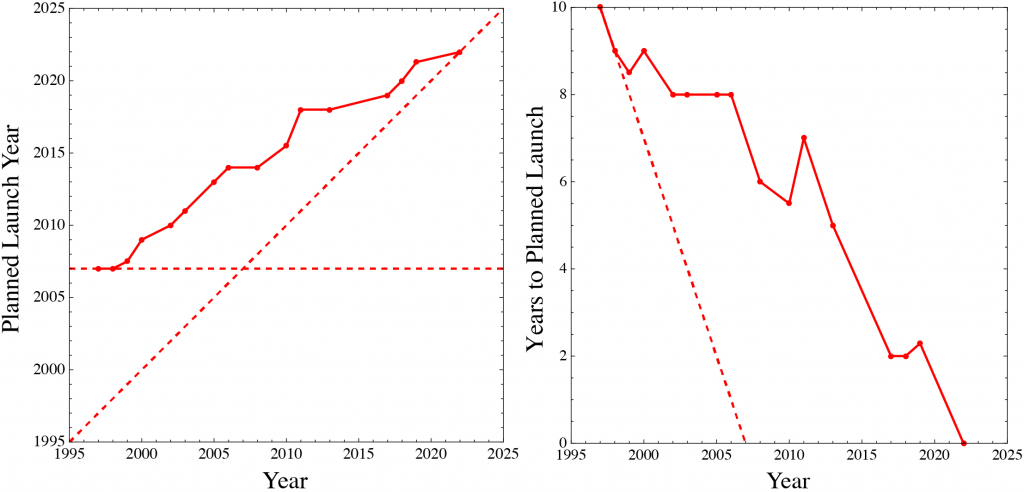



Thanks, Mark! I enjoy reading your posts as well.