In 1609, Johannes Kepler first described how planets orbit the sun in ellipses. Kepler understood an ellipse as both the locus of points whose distances from two foci sum to a constant and as the intersection of a cone and a plane. But how are these familiar definitions equivalent?
In 1822, Germinal Dandelin discovered a beautiful construction that proves this classic equivalence. The looping animation below pauses periodically to emphasize key aspects of the proof.
A plane intersects a cone in a black ellipse. The red and cyan spheres are tangent to the cone at the parallel circles and tangent to the plane at the ellipses’ focal points. The red lines are equal because they are tangent to the red sphere from the same point; same for the cyan lines. The sum of the cyan and red lines is both the sum of the distances of an ellipse point from the foci and the fixed distance along the cone between the red and cyan tangent circles.
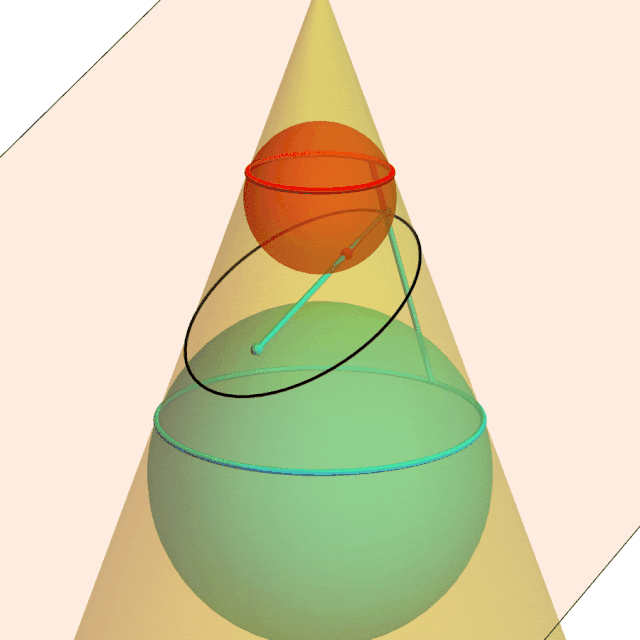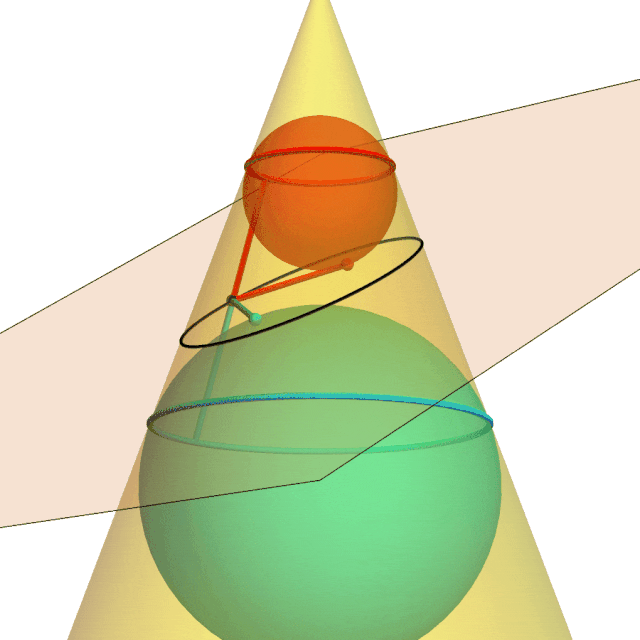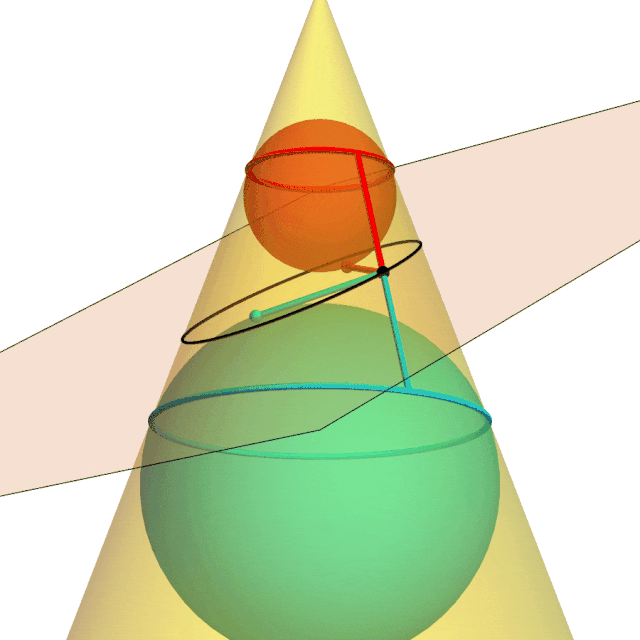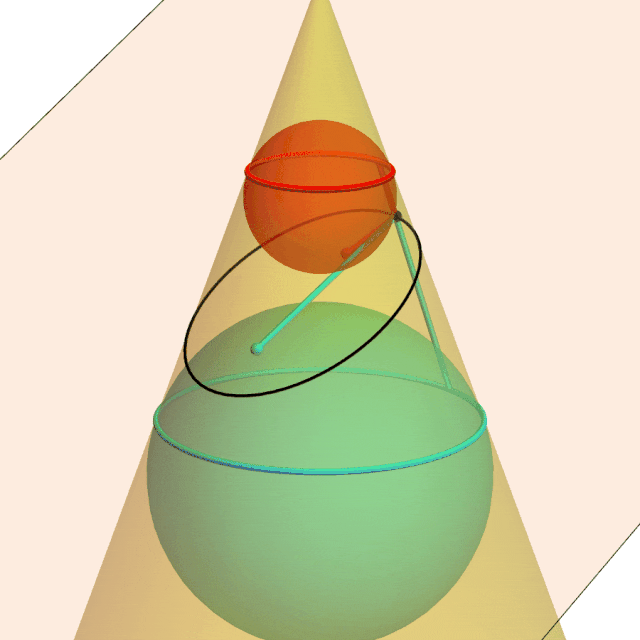
Dandelin spheres illustrate why the intersection of a plane and a cone is the set of points the sum of whose distances from two fixed points is constant.
