Fermions like electrons, protons, and neutrons inhabit a 720° world: 360° rotations negate their quantum states, but 720° rotations restore them.
A simple macroscopic model of such spinors is an arrow translating on a Möbius strip: as the center circle rotates, the attached arrow flips after 360° but flips back after 720°.
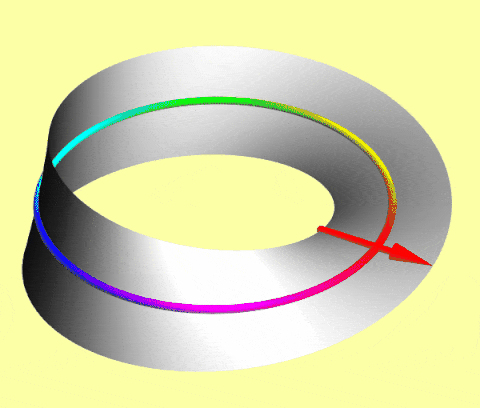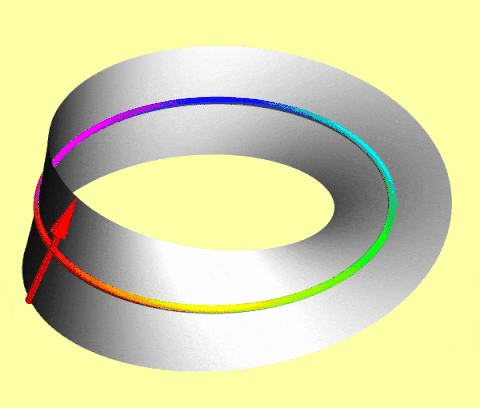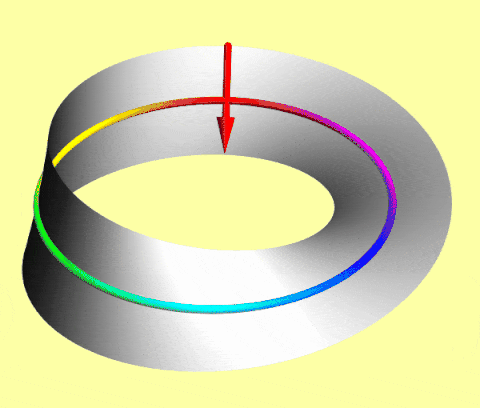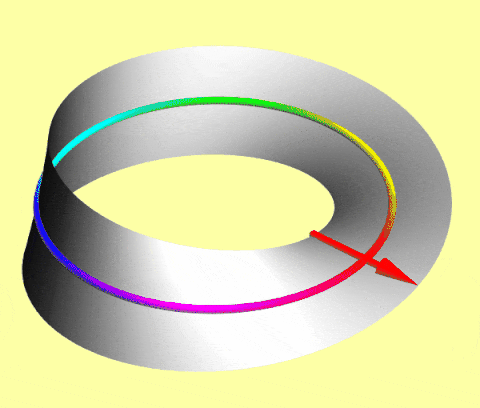
In Dirac notation
R_{2\pi}|\psi \rangle = -|\psi \rangle = e^{i \pi}|\psi \rangle,but
R_{4\pi}|\psi \rangle = +|\psi \rangle= e^{i 2\pi}|\psi \rangle,where the ket |\psi\rangle is the state, the exponentials are phase factors, and their arguments are phase shifts.
To detect a relative phase shift, send a neutron via two paths, rotate it along one path with a magnetic field (coupled to its magnetic dipole moment), and observe destructive interference for 360° rotations and constructive interference for 720° rotations. (The experiment is harder with charged electrons and protons, whose translation is deflected by the magnetic field.)

Thanks, Mark! I enjoy reading your posts as well.