Despite growing up in three dimensions, as a kid I did not recognize one of 3D’s deep and subtle properties: full rotations tangle, but double rotations untangle!
Following physicist Paul Dirac, twist a belt one full turn about its length. The 360° single twist cannot be undone without changing the belt buckles’ orientations, although the twist can be changed from clockwise to counterclockwise. Now twist the belt two full turns about its length. Amazingly, the 720° double twist can be undone without changing the belt buckles’ orientations. The double twist is the true identity.
The animations below show belts twisting concretely in 3D space and abstractly in a 3D projection of the 4D quaternion unit sphere. Points on the sphere represent all 3D rotations (twice). Each blue dot represents a belt cross section rotation and is located by a radius vector. Suppressing rotations about the 1‑direction, the radius vector’s projection onto the 2-3-plane is the section’s rotation axis and twice its co-latitude is the section’s rotation angle.
The sphere’s north and south poles represent the same orientation, 0° ≡ 720° and 360°, but different orientation-entanglements. Identifying the north and south poles as the same orientation allows closed loops on the quaternion sphere to represent both 360° and 720° belt twists, but only the latter can smoothly contract to the north pole identity rotation. This multiple connectivity is reminiscent of a torus (or donut with hole), where toroidal loops (around-the-hole) are contractible but poloidal (through-the-hole) loops are not, rather than the simple connectivity of a sphere, where all loops are contractible.
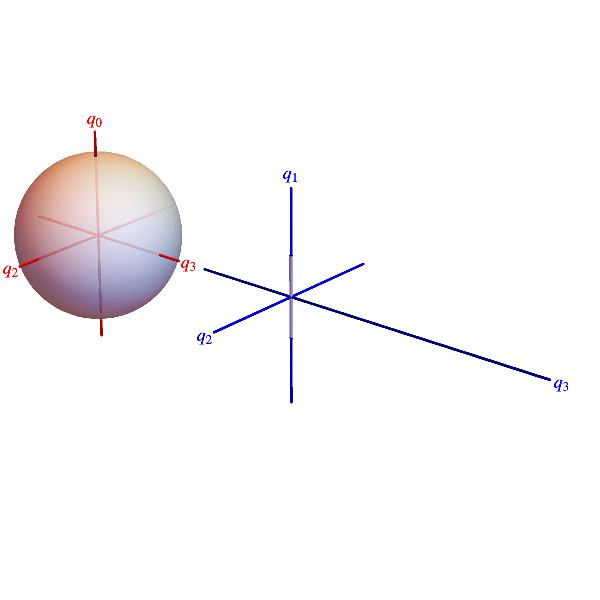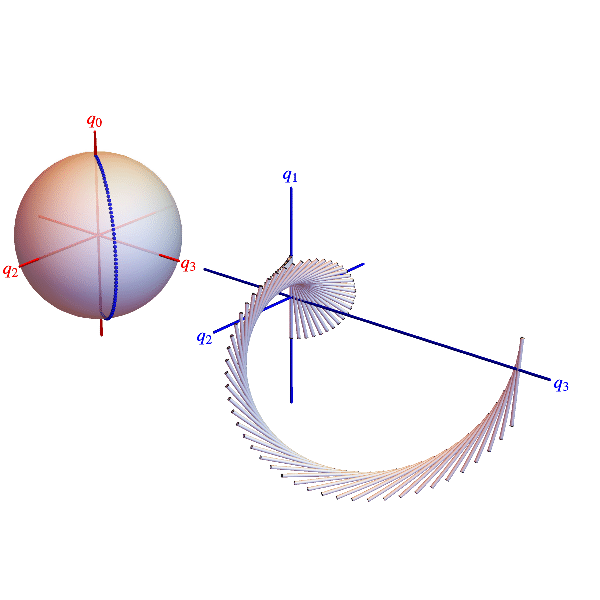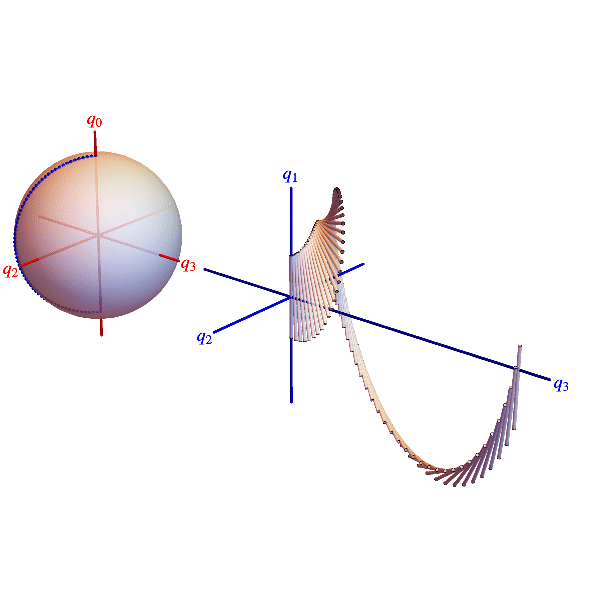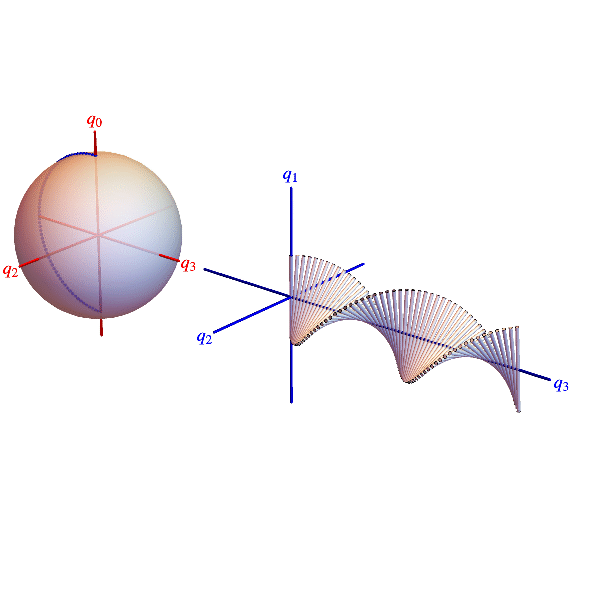
Elastic belt with a 360° twist. Blue dots on quaternion sphere projection represent belt cross section rotations. Blue curve connecting dots can not be smoothly contracted to the untwisted state represented by the north pole, but without changing the orientation of the belt’s ends, the twist can be changed from clockwise to counterclockwise as indicated.
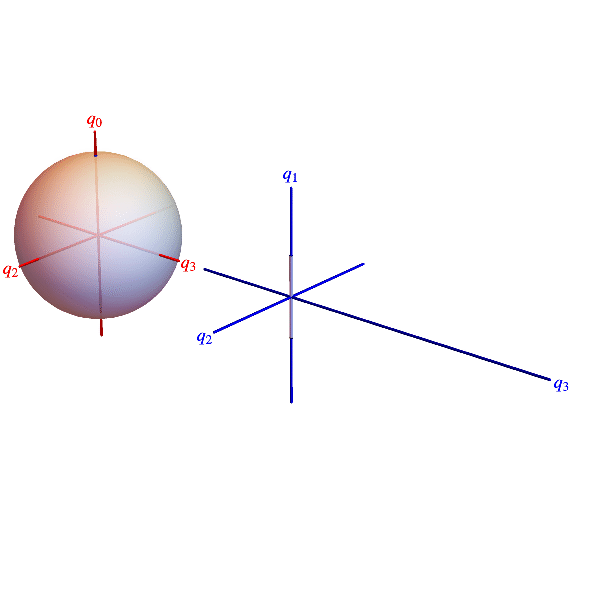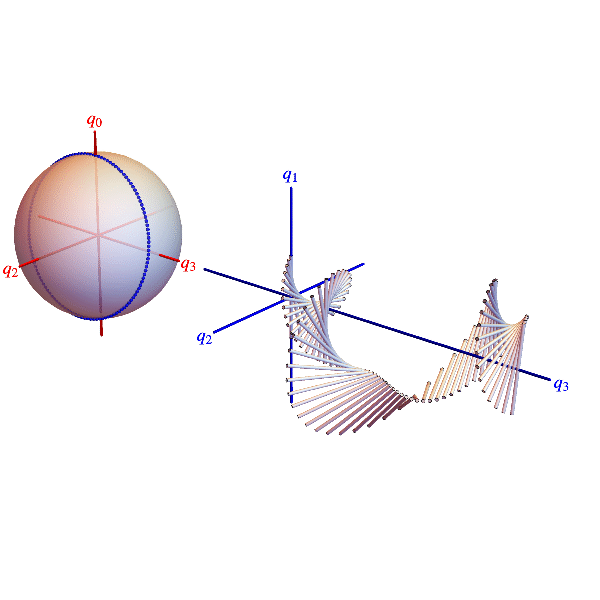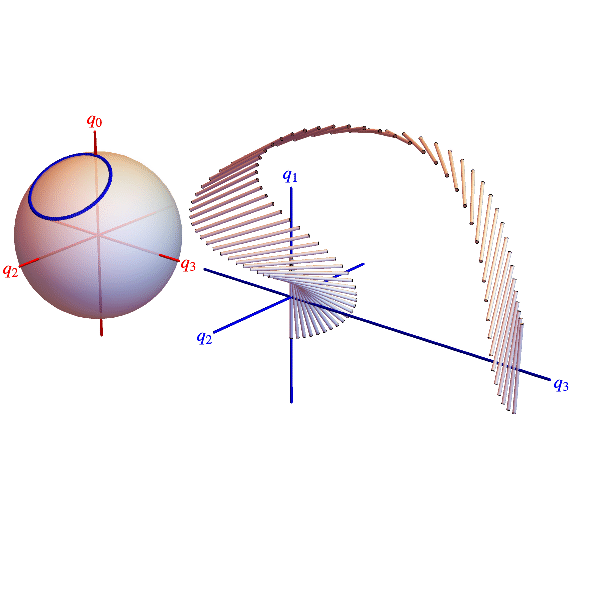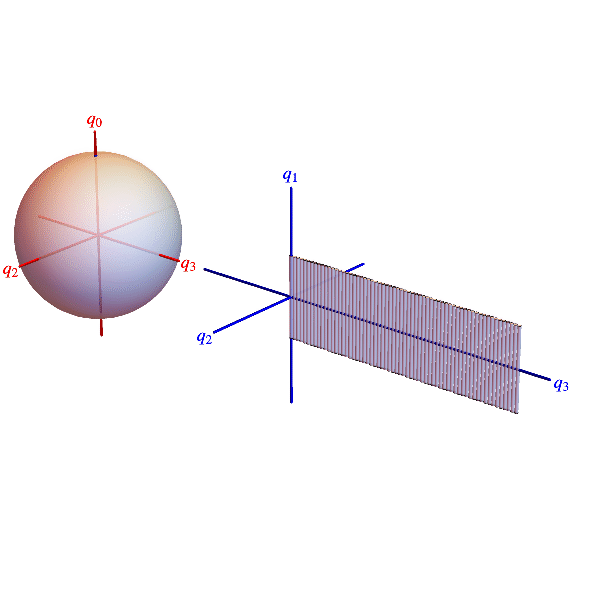
Elastic belt with a 720° twist. Blue dots on quaternion sphere projection represent belt cross section rotations. Blue curve connecting dots can be smoothly contracted to the untwisted state represented by the north pole, so without changing the orientation of the belt’s ends, the twist can be be undone as indicated.



About the connectivity of the torus, setting aside that it would have to intersect itself, the torus can be turned inside-out, swapping the outside hole and the inside hole, so it would seem that around-the-hole loops are as contractible as through-the-hole loops, that is they aren’t.
Here’s a Windows program called “Antitwister” that displays a good animation of Dirac’s theorem along with related motions:
http://ARIwatch.com/VS/Algorithms/Antitwister.htm