Norton’s Dome is a fascinating counterexample in classical mechanics: A frictionless mass balanced at the dome’s top can remain there forever — but can also spontaneously slide down!
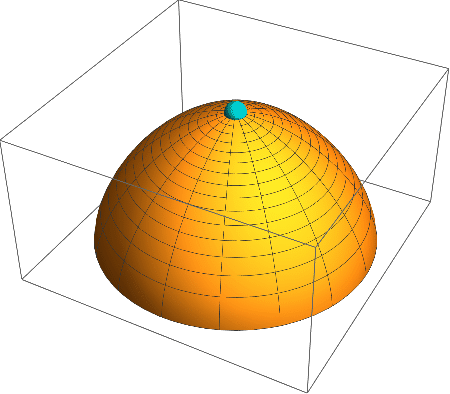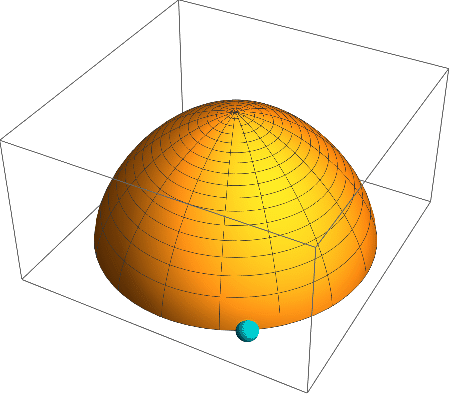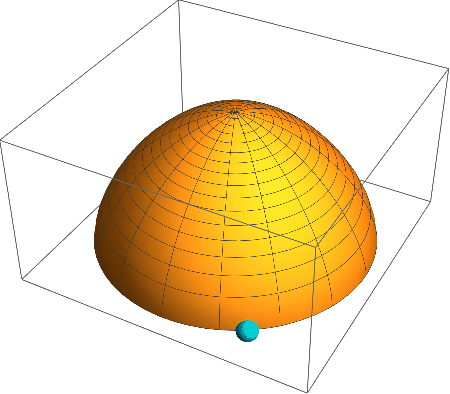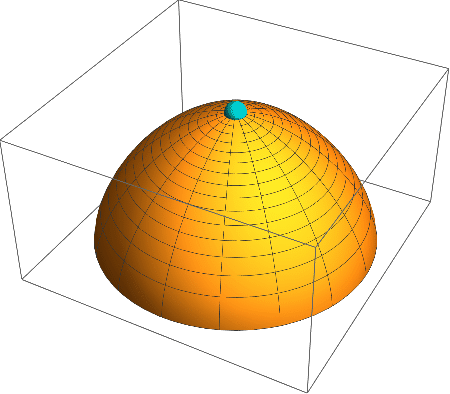
A mass slides down Norton’s dome from rest and then is kicked back up to rest.
The Shape
Norton’s dome has a cubed square root profile: if the downward height is z at dome arc length s, then
\frac{z}{z_m} = \left(\frac{s}{s_m}\right)^{3/2}.f max height z_m = 2/3 when max arc length s_m = 1, then
z = \frac{2}{3}s^{3/2}.By the Pythagorean theorem, ds^2 = dx^2 + dz^2, and so
x = \int dx = \int \sqrt{ds^2 – dz^2} =\int ds \sqrt{1 – \left(dz/ds\right)^2} = \int_0^s ds \sqrt{1 – s}.Integrate to find the horizontal coordinate in terms of the arc length
x = \frac{2}{3}\left(1 – \left(1-s\right)^{3/2}\right),and inversely
s = 1 – \left(1 -\frac{3}{2}x\right)^{2/3}.Eliminate the arc length to find the profile
x =\frac{2}{3}\left(1 – \left(1-\left(\frac{3}{2}z\right)^{2/3}\right)^{3/2}\right),and inversely
z =\frac{2}{3}\left(1 – \left(1-\frac{3}{2}x\right)^{2/3}\right)^{3/2}.If the arc length 0\le s \le 1, then the rectangular coordinates -2/3 \le x,y \le 2/3 and 0\le z \le 2/3.
The IVP
For sliding frictionlessly on the dome, form the total energy as the sum of the kinetic and potential energies
E = T + V = \frac{1}{2} m v_s^2 – m g z = \frac{1}{2}\dot{s}^2 – \frac{2}{3} s^{3/2},for unit mass and gravity. Differentiate with respect to time to get
0 = \dot{s} \ddot{s} – s^{1/2}\dot{s}and divide by \dot s to get the equation of motion
\ddot{s} = \sqrt{s}.Alternately, form the Lagrangian as the difference in the kinetic and potential energies
L = T – V = \frac{1}{2} \dot{s}^2 + \frac{2}{3} s^{3/2}Alternately, form the Lagrangian as the difference in the kinetic and potential energies
L = T – V = \frac{1}{2} \dot{s}^2 + \frac{2}{3} s^{3/2}and insert into Euler-Lagrange equation
\frac{d}{dt} \frac{\partial L}{\partial \dot{s}} = \frac{\partial L}{\partial s}to again get
\ddot{s} = \sqrt{s}.The acceleration along the dome increases as the square root of the arc length. Combine the equation of motion with the initial conditions s[0]=0 and \dot{s}[0]=0, corresponding to a mass at rest on top of the dome, to form an initial value problem (IVP).
The Solutions
Surprisingly, two solutions exist: infinite rest
s[t] = 0and spontaneous sliding
s[t] = \frac{1}{144} t^4.To check the latter, differentiate to get
\dot s = \frac{1}{36} t^3, \ddot s = \frac{1}{12} t^2 = \sqrt{s}.How can a physical system have two evolutions?
The Resolution
If an IVP’s equations are continuous, solutions exist; if the first derivatives are also continuous, the solution is unique. In this case, the square root \sqrt{s} in the equation of motion means that the first derivative is not continuous at the origin, so solutions exist but are not unique.
The peak of Norton’s Dome is continuous, and its slope is continuous, but the slope of its slope is discontinuous. The apex of a cone is more extreme, as its slope is discontinuous.

One response to “Norton’s Dome”
In Physics we often encounter multiple solutions to mathematical problems and just discard those deemed to be non-real.
Also, why only take +ve roots ?