Anholonomy

A falling cat’s twisting returns its shape to normal but rotates its body to land feet down. Earth’s spin returns a Foucault pendulum to its initial position in one day but rotates its oscillation plane. Parallel parking cyclically rotates a car’s front wheels but shifts the car sideways. These are examples of nonholonomic motions or mechanical anholonomies.

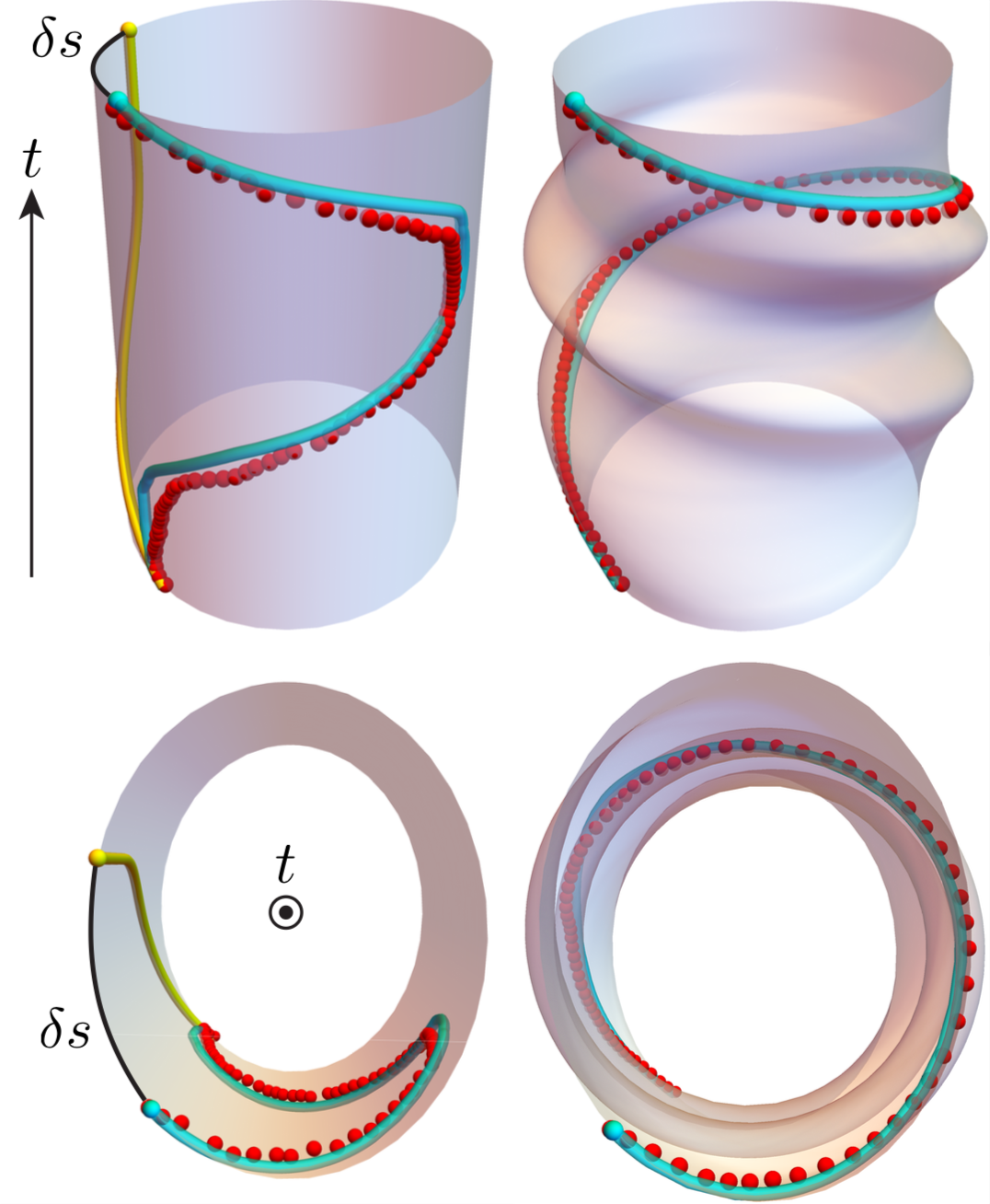
Hwan Bae, Norah Ali, and I just published a featured article in the journal Chaos on another famous anholonomy, Hannay’s hoop, which involves a bead sliding frictionlessly on a horizontal noncircular hoop: A slow cyclic rotation restores the hoop to its original state but unavoidably shifts the moving bead by an angle that depends on the hoop’s geometry. Rotating a noncircular hoop indelibly imprints its geometry on the bead’s motion.

In the limit of slow rotation and fast beads, the shift is called Hannay’s angle (and is analogous to Berry’s phase in quantum mechanics). We mathematically generalized the shift to any speed, fast or slow, and were able to observe it in a simple experiment involving wet ice cylinders sliding in 3D printed channels.