Historically, astronauts have launched roughly east to exploit Earth’s spin, as the terrestrial equator moves at nearly 1000 mph with respect to its center. But last week the Fram2 SpaceX Dragon crew launched south from the Kennedy Space Center to become the first humans to orbit Earth over its poles.
The all-private, all-international, rookie crew consisted of entrepreneur and mission commander Chun Wang, cinematographer and Dragon commander Jannicke Mikkelsen, roboticist and Dragon pilot Rabea Rogge, and polar guide and medical officer Eric Philips. None of the crew were pilots, let alone professional astronauts, but they all had deep ties to polar exploration and each other, meeting at the Svalbard, Norway archipelago, one of Earth’s northernmost inhabited regions. Indeed, their mission was named after the Norwegian sailing ship Fram, which explored both poles circa 1900, and the crew carried a small wooden piece of Fram with them.
The Fram2 crew performed 22 experiments from a list offered by SpaceX to help the company prepare for trips to Mars and beyond. One of these involved taking medical X-ray photographs in space, which on long spaceflights might help diagnose and repair injuries in people and faults in equipment. Another was high-resolution videography of Earth from their unique orbital perspective. Still another was the crew’s unassisted egress of the Dragon capsule shortly after splashdown.
I especially enjoyed Chun’s social media updates, enabled via a laser connection to the Starlink satellite internet constellation. After adapting to microgravity, the crew seemed to enjoy themselves immensely and reported sleeping well. Addition of the cupola not only provided stunning views but notably expanded Dragon’s interior volume. The inspiring Fram2 mission expanded the human spaceflight envelope, advanced spaceflight privatization, and laid groundwork for extended spaceflight to Moon, Mars, and beyond.

Professional cinematographer and Dragon commander Jannicke Mikkelsen using a Red Digital Cinema Raptor 8K video camera in the Dragon’s cupola.
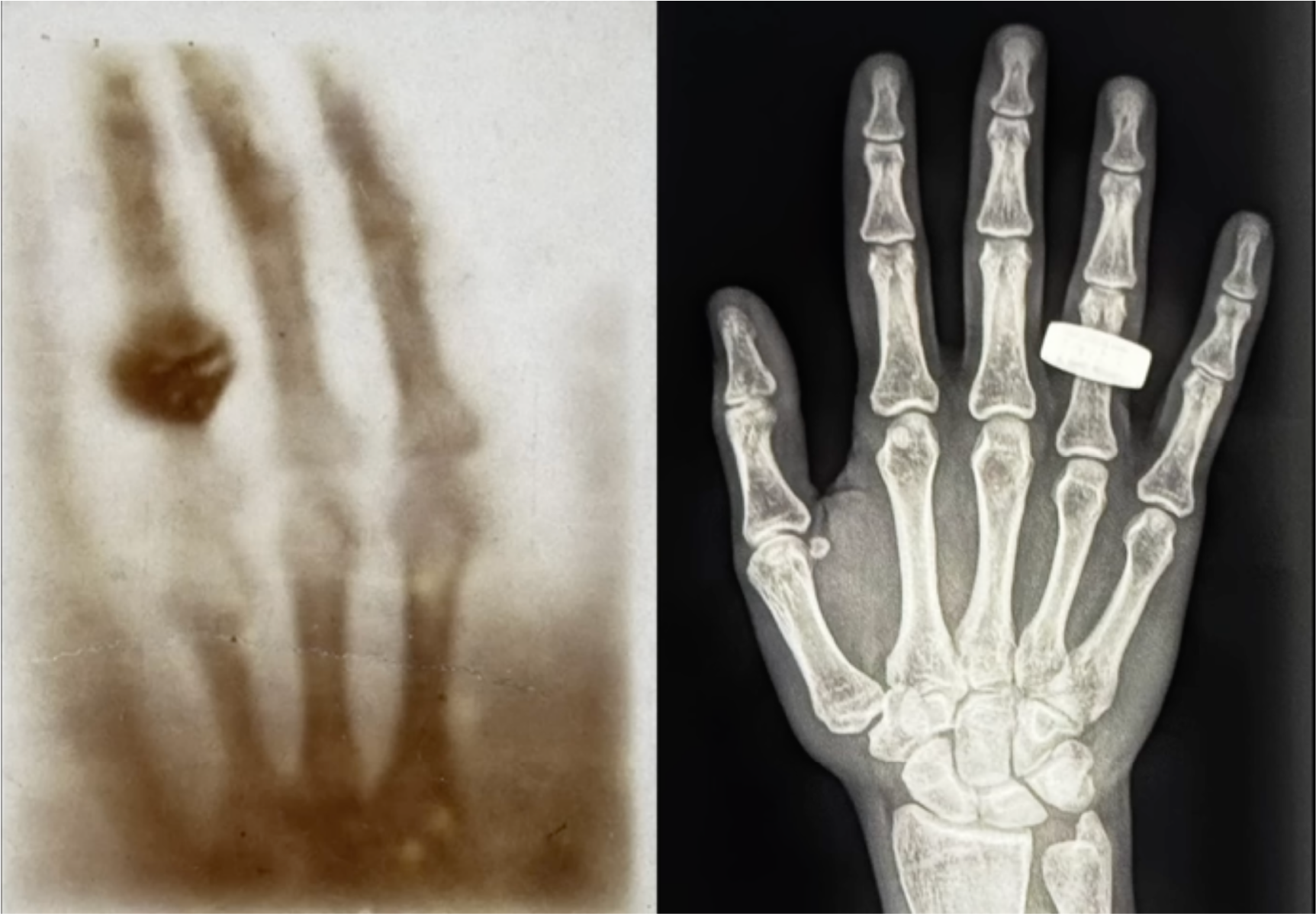
X-ray photo on Earth by W. C. Röntgen in 1895 (left) and X-ray photo off Earth by the Fram2 crew in 2025 (right).


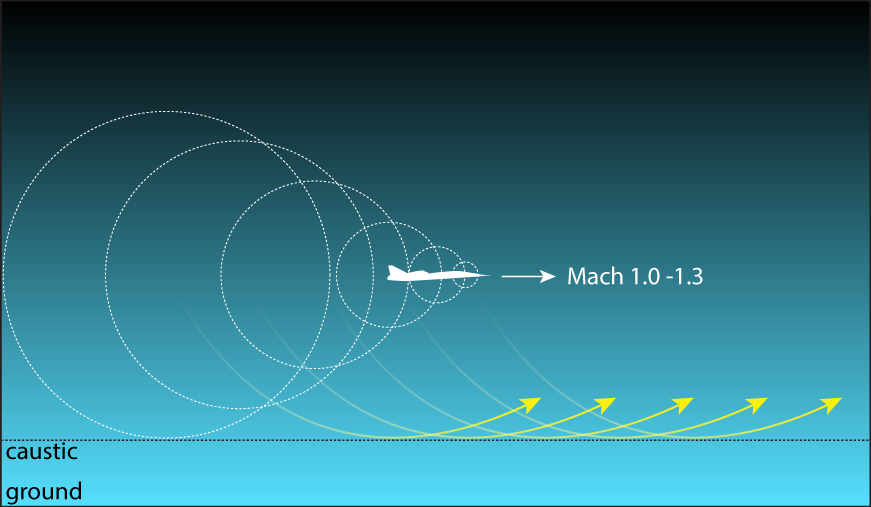
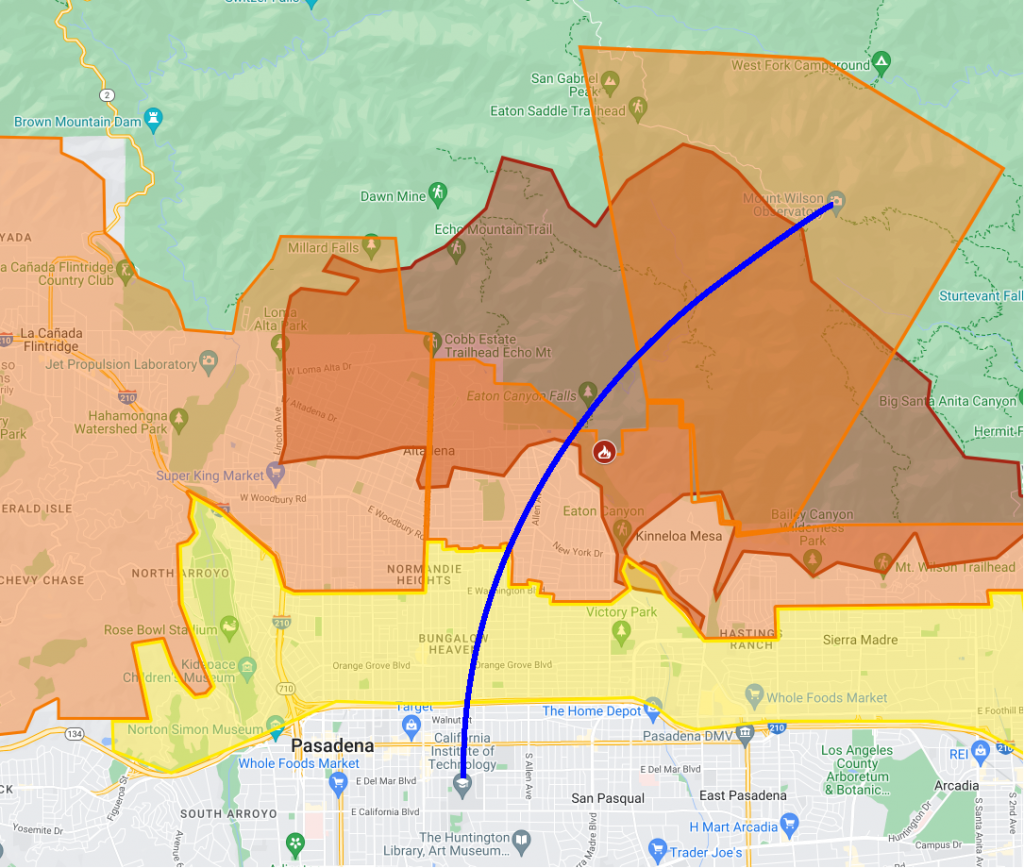
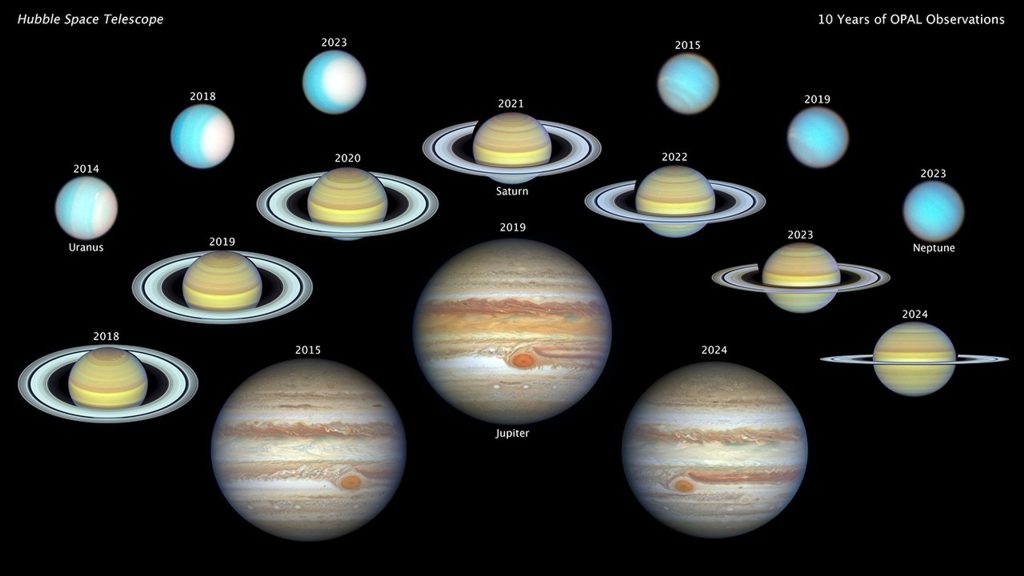







Thanks, Mark! I enjoy reading your posts as well.