Since childhood I have been fascinated by M. C. Escher‘s extraordinary graphics. Escher once wrote, “I never feel quite at home among my artist colleagues; what they are striving for, first and foremost is “beauty” … I guess the thing I mainly strive after is wonder … .”
In 1945 Escher produced a lithograph called “Balcony“, of buildings overlooking a Malta harbor, whose center is enlarged four times compared to its edges to emphasize a single balcony. Working without computers, Escher accomplished the inflation by first manually constructing a blowup of a square grid.
Later he imagined “a cyclic expansion or bulge, without beginning or end”. The result was his amazing 1956 lithograph “Print Gallery“, one of his favorite prints, and one of two that I have on the walls beside me as I write this. A young man in a print gallery gazes up at a print of a Malta harbor town, and as we follow his gaze rightward the scene enlarges until we see a woman looking out a window above the entrance to the print gallery containing the man — who is simultaneously inside and outside it!
Like the circular bulge of “Balcony”, Escher accomplished the cyclic bulge of “Print Gallery” by first transforming a grid of squares, intuitively ensuring that right angles were mapped to right angles. The transformed squares became very small near the print’s center, and Escher left that part blank.
In 2003, mathematicians B. de Smit and H. W. Lenstra Jr. published a refinement and extension of “Print Gallery” that filled the center with an infinite regress of rotated and scaled down copies of itself. Using complex variables
z = x + i y = r e^{i \theta} \in \mathbb{C},and noting that moving 256 units in the original square grid corresponded to moving 22.6 units and rotating 158° in the cyclic bulge, they defined the conformal mapping
h(z) = z^\alpha = \exp(\alpha \log z)by
h^{-1}(256)\approx 22.6\, e^{-i\, 158^\circ},which has the principle branch solution
\alpha \approx 1.33\,e^{-i\,41.4^\circ},as in the figures below.
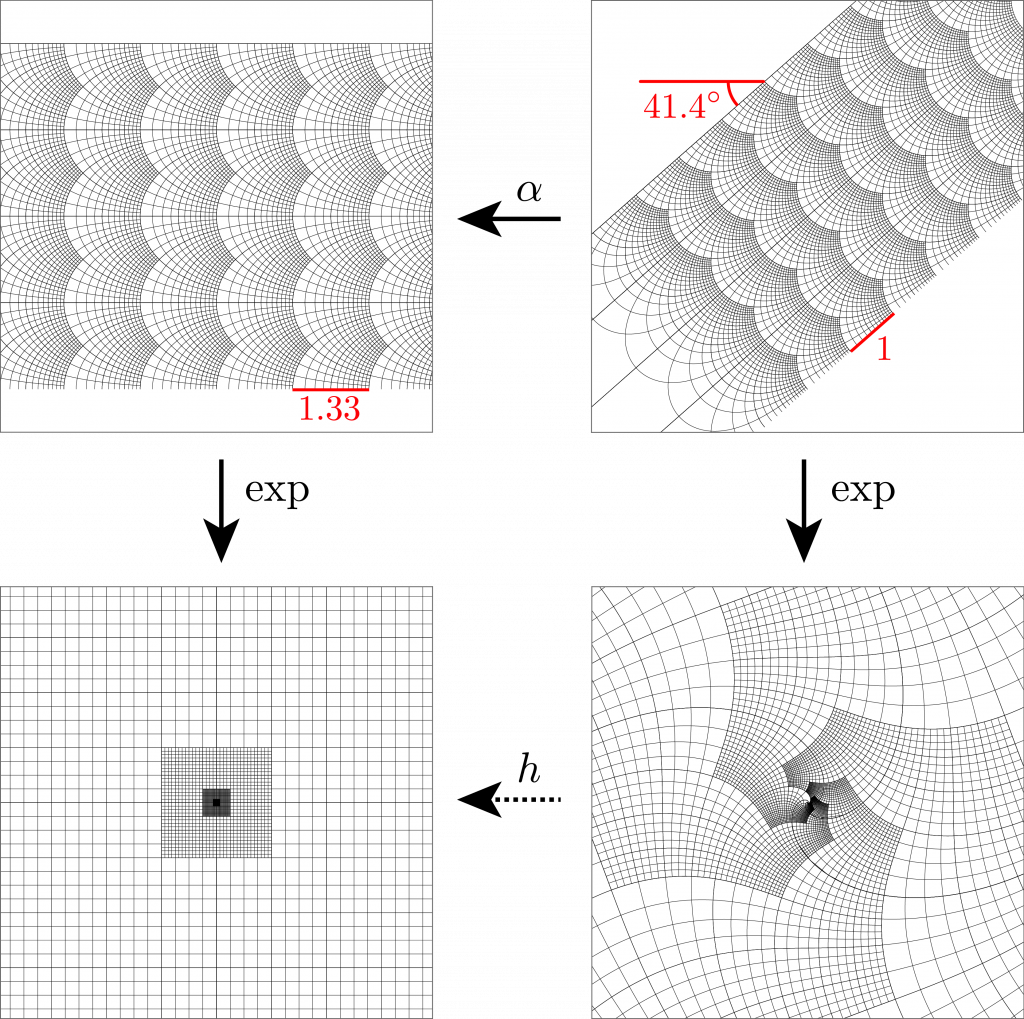
Conformal map underlying the cyclic bulge (and inward spiral) of Escher’s “Print Gallery” is multiplication by the complex constant \alpha in the exponent.

Escher’s “Print Gallery” as refined and extended by de Smit and Lenstra. The observer is both inside and outside the print!
