Today, about six years after beginning the relevant research, my colleagues and I were issued United States Patent No. US 12 450 468 B2, “Physics augmented neural networks configured for operating in environments that mix order and chaos”. The work began during my 2019-2020 sabbatical at the Nonlinear Artificial Intelligence Lab at North Carolina State University and continued for two years, across the four publications listed below, accompanied by years of legal work by NCSU.
Neural networks are powerful computational tools but they can be confounded by the mix of order and chaos in natural and artificial phenomena. Our solution to this “chaos blindness” exploits an elegant and deep structure to everyday motion discovered by William Rowan Hamilton, who remarkably re-imagined such motion as an incompressible energy-conserving flow in an abstract, higher-dimensional space of positions and momenta. In this phase space, motions are unique trajectories confined to constant-energy surfaces, and regular motions are further confined to donut-like hypertorii. This structure constrains our Hamiltonian neural networks to better forecast systems that mix order and chaos, such as the Hénon-Heiles motion of stars in galaxies.
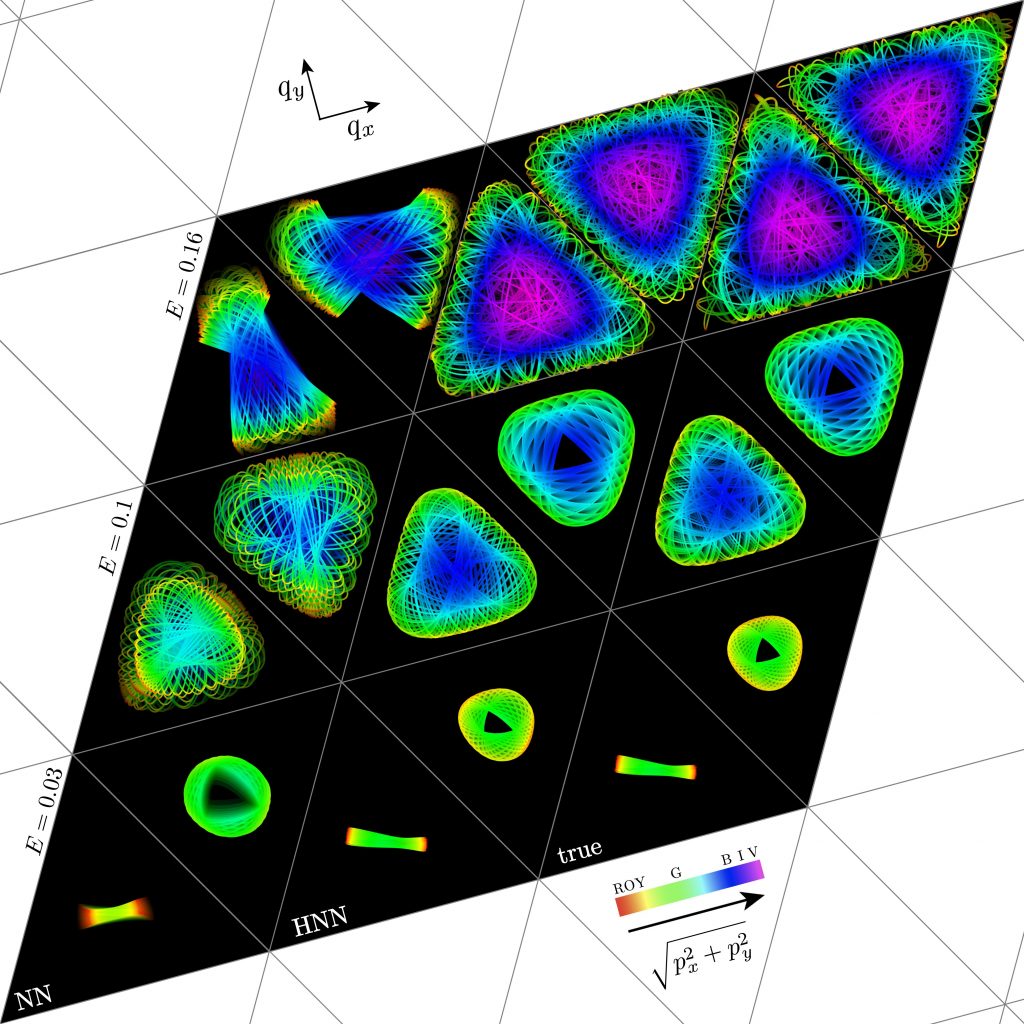
Two sample Hénon-Heiles flows for different initial conditions forecast by conventional neural network (left), Hamiltonian neural network (center), and Hénon-Heiles differential equations (right), for small (bottom), medium (middle), and large (top) bounded energies. Hues code momentum magnitudes, from red to violet; orbit tangents code momentum directions. Orbits fade into the past.
Physics enhanced neural networks learn order and chaos, A. Choudhary, J. F. Lindner, E. G. Holliday, S. T. Miller, S. Sinha, W. L. Ditto, Physical Review E, volume 101, pages 062207(1-8) (June 2020) doi.org/10.1103/PhysRevE.101.062207
The scaling of physics-informed machine learning with data and dimensions, S. T. Miller, J. F. Lindner, A. Choudhary, S. Sinha, W. L. Ditto, Chaos, Solitons & Fractals: X, volume 5, pages 100046(1-7) (2020) doi.org/10.1016/j.csfx.2020.100046
Forecasting Hamiltonian dynamics without canonical coordinates, A. Choudhary, J. F. Lindner, E. G. Holliday, S. T. Miller, S. Sinha, W. L. Ditto, Nonlinear Dynamics, volume 103 number 2, pages 1553-1562 (2021) doi.org/10.1007/s11071-020-06185-2
Negotiating the separatrix with machine learning, S. T. Miller, J. F. Lindner, A. Choudhary, S. Sinha, W. L. Ditto, Nonlinear Theory and Its Applications, volume 12, number 2, pages 1-9 (April 2021) doi.org/10.1587/nolta.12.134

Thanks, Mark! I enjoy reading your posts as well.