Logic with Nonlinear Maps

In 1999, Bryan Prusha ’98 and I wrote an article for Physics Letters A illustrating why logic requires nonlinearity. Recently, with Bill Ditto, I revisited this theme by demonstrating how to encode all 16 binary boolean (true-false) functions in single iterations of a unimodal map, just published in Physica D. These encodings may facilitate the next generation of dynamics-based computation.

More specifically, we encode binary logic gates in single iterations of step functions of unimodal maps of affine transformations of inputs. Define a boolean function family from \{0,1\}\times\{0,1\}\rightarrow \{0,1\} by the composition

g_{\vec p} = H \circ f\circ a_{\vec p},

or equivalently

g_{\vec p}\,(x,y) = H\bigg(f\Big(a_{\vec p}\,(x,y)\Big)\bigg),

where

H(f) = \mathbf{1}_{f\ge 0} = \left\{\begin{array}{ll} 0, & f < 0, \\ 1, & f\geq 0, \end{array}\right.

is the Heaviside step function,

f(z) = 4 z (1-z)

is the nonlinear, unimodal, logistic map, and

a_{\vec p}\,(x,y) = p_1 + p_2 x + p_3 y

is an affine transformation of the boolean input variables \{x,y\} \in\{0,1\}^2 and a linear function of the real parameters \vec p = {p_1,p_2,p_3} \in [-1,1]^3.

For example, if p_3 = 1/2, then there exists open sets of p_1, p_2 that encode all 6 common logic gates AND, OR, XOR, NAND, NOR, XNOR, as in the figure below.

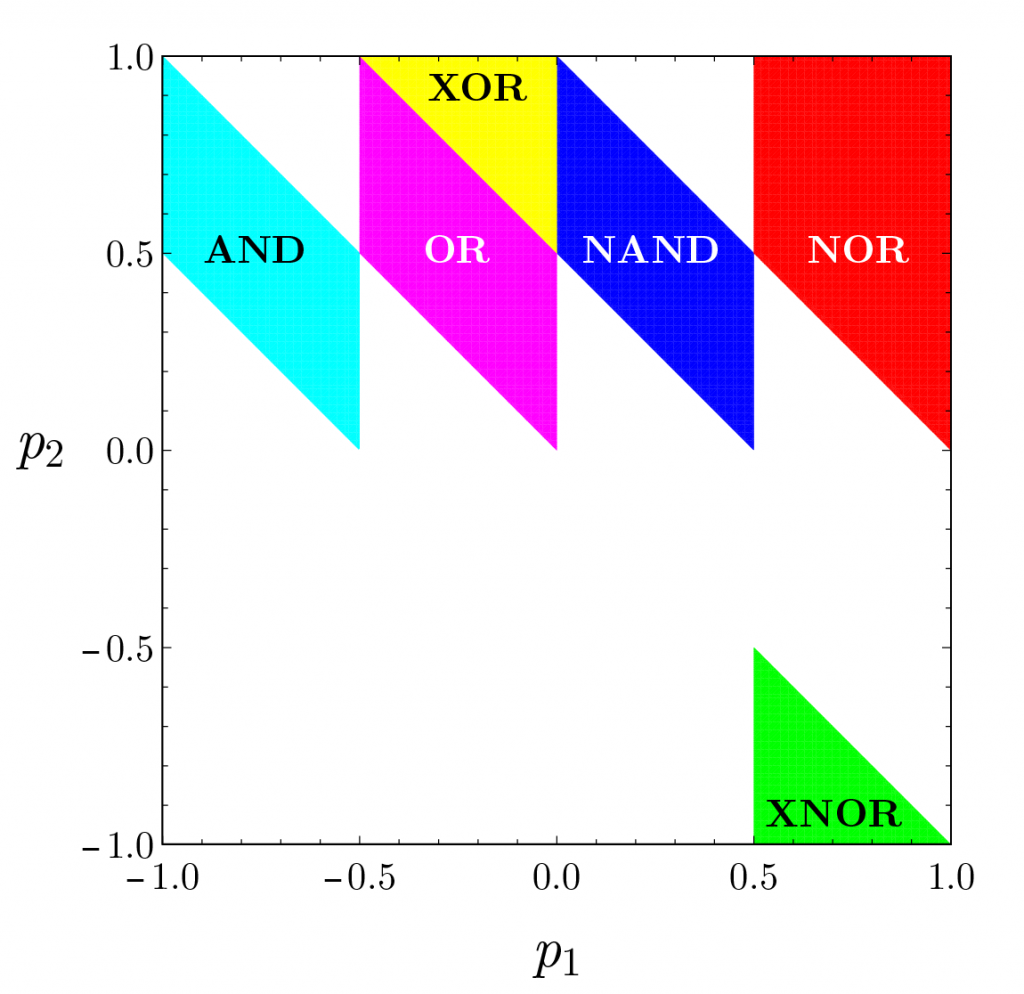
Parameters p_1,p_2 that realize 6 common binary logic gates for p_3=1/2.

My favorite sentence in the article is, “Chaotic dynamics can obfuscate computation for increased security, but like Shakespeare’s engineer ‘Hoist with his own petard’, are chaogates subverted by chaos itself?” You don’t always get to quote Shakespeare in a physics article! (But you’ll need to read the article for the answer.)