After the conference in Switzerland, I stopped in Tübingen, Germany to visit Otto Rössler. Nearly everyone who learned about nonlinear systems knows the nowadays named Rössler attractor and his work in chaos theory in the 1970s.
For the last four years we were in contact for my science history project and this year, I finally visited him. We had a great day and I received MANY documents from conferences 40-50 years ago. He saved ‘everything’ in countless binders, sorted by years, and kept them in ceiling-heigh bookshelfs at his home.

Otto Rössler and Niklas Manz on 20 July 2024 at Schwärzlocher Hof (farm and restaurant), which started as an abbey circa 1100.

Otto and Reimara Rössler on 20 July 2024 at Schwärzlocher – with the local peacock mom.
In the 1970s, Otto Rössler designed a famous 3D flow that mimics the folding and bending of taffy in a taffy machine, which is now named the Rössler attractor. Described by the 3 coupled differential equations
\begin{aligned}\dot x &= \vphantom{}-y-z, \\ \dot y &= x + a y,\\ \dot z &= b-c z + x z,\end{aligned}with just one nonlinear term, the x z in the third equation. The Rössler velocity field results from the interaction of two crossed vortices, one near the origin and the other far away pointing at the “fold” in the Rössler band. The parameter space \{a,b,c\} is large, but the system undergoes a period-doubling route to chaos in \{0<a<2, b=2, c=4\}, as in the animation below, which culminates in a period-3 window.
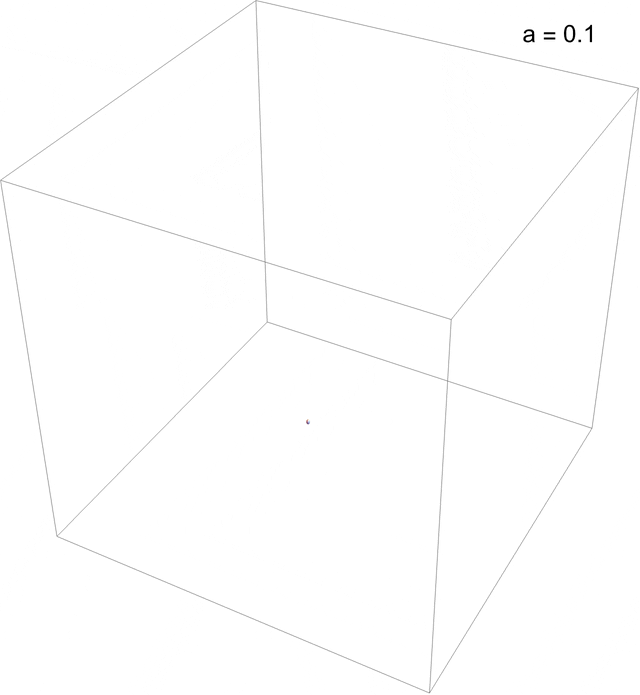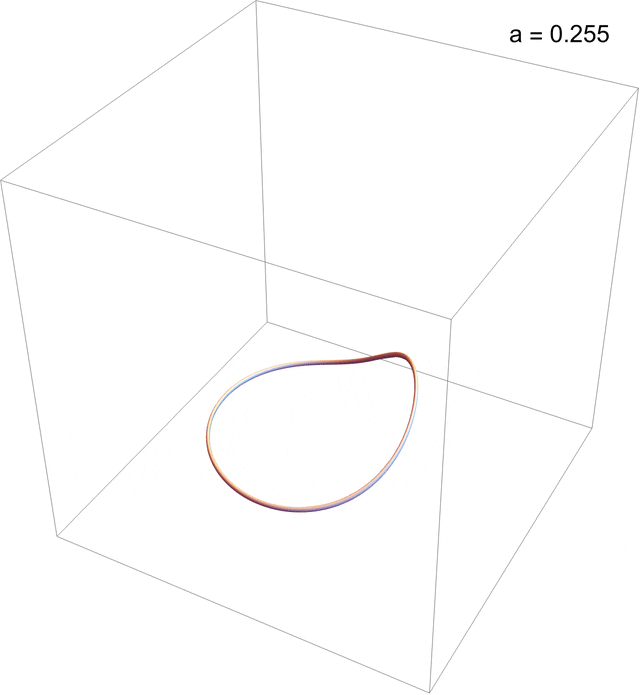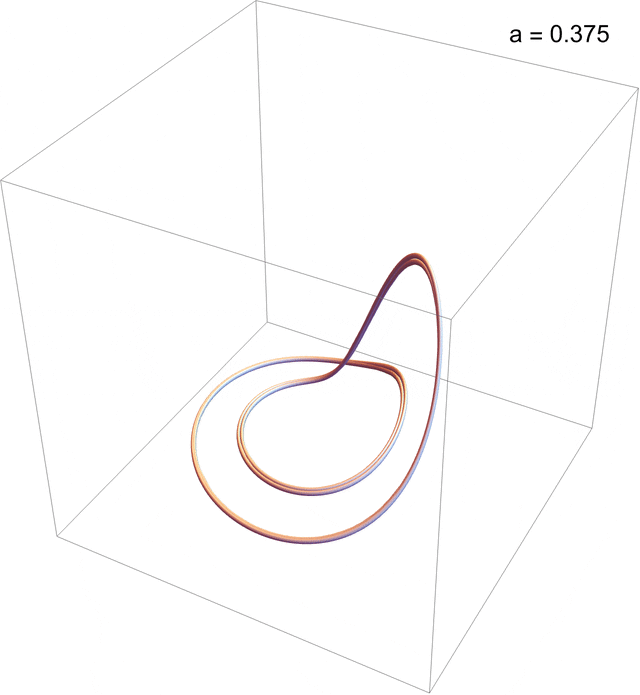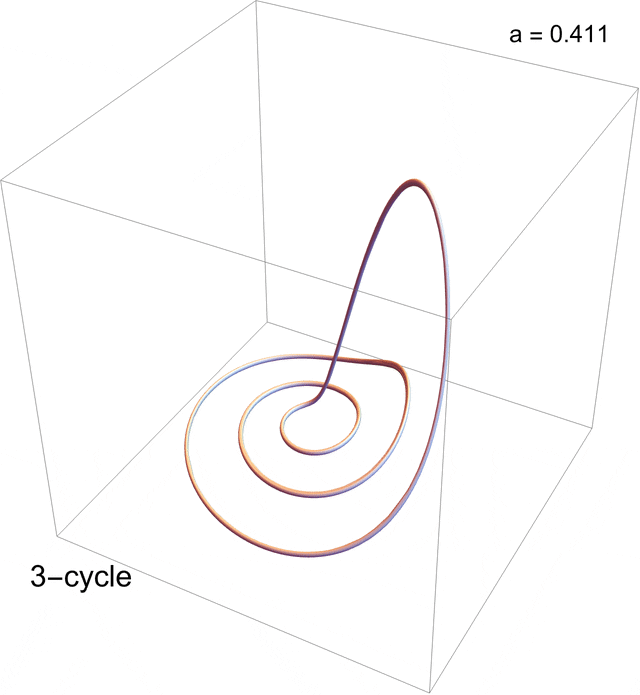
Post-transient {x ,y, z} solutions to the Rössler system for 0.1 < a < 0.411, b = 2, c = 4, exhibiting a period-doubling route to chaos culminating in a 3-cycle window. (You may need to “click” on the figure to see the animation.)
The animation was created by John Lindner.

Thanks, Mark! I enjoy reading your posts as well.