When searching for prime numbers, the next prime number is no larger than twice the current number. Postulated by Joseph Bertrand, first proved by Pafnuty Chebyshev, I present an elementary proof based on one by the teenage Paul Erdős.
Erdős was one of the most prolific twentieth century mathematicians, publishing about 1500 articles with more than 500 coauthors. (Indeed, my Erdős number, or collaboration distance, is 5.) Reportedly, Erdős liked to talk about The Book, in which God maintains the perfect proofs for mathematical theorems. Like Aigner & Ziegler’s presentation in their Proofs from The Book, my “illustrated” version is a modest attempt at such a proof, a deep result proved by elementary means: bounding the central binomial coefficient (2n)! / (n!n!) above and below exposes the necessity of primes p for all n < p \le 2n. Enjoy!
Some Notation
In analogy with the factorial function
n! = \prod_{m\le n} mas the product of all positive integers m not greater than n, define the primorial function
n\# = \prod_{p\le n} pas the product of all primes p not greater than n. Recall the binomial function
\binom{n}{m} = \frac{n!}{m!(n-m)!}and the floor function
\lfloor x\rfloor =\max\{n\in \mathbb {Z} \mid n\leq x\}.Primorial Function Upper Bound
The primorial function is upper bounded by the exponential
x\# = \prod_{p\le x}p \le 4^{x-1} < 4^x.Proving this for the largest prime q < x is sufficient, as the substitution unchanges the left side and lowers the right side. For x = 2, the bound 2 < 4 is correct. For induction, assume it’s true for primes x < 2m and for x = 2m+1 split the product
(2m+1)\# = \prod_{p\le 2m+1} \hspace{-0.7em}p = \prod_{p\le m+1} \hspace{-0.5em}p\ \prod_{m+1 < p\le 2m+1} \hspace{-1.7em}p\hspace{1em}.The first factor is bounded by the induction hypothesis. For the second factor, consider the binomial expansion
2^{2m+1}=(1+1)^{2m+1}=\sum_{k=1}^{2m+1}\binom{2m+1}{k} =\cdots + \binom{2m+1}{m} + \binom{2m+1}{m+1} + \cdots \ge \binom{2m+1}{m} + \binom{2m+1}{m+1} = 2\binom{2m+1}{m},where the two central binomial coefficients are equal (as in Pascal’s triangle). But the integer
\binom{2m+1}{m} = \frac{(2m+1)!}{m!(m+1)!} = M \prod_{m+1 < p\le 2m+1} \hspace{-1.6em}p \hspace{1em}\ge \prod_{m+1 < p\le 2m+1} \hspace{-1.6em}p\hspace{1.2em},where the integer M>1, as the bounded primes p divide the numerator but not the denominator. Combine these results to get
(2m+1)\# \le4^m \cdot 2^{2m} = 4^{2m}as desired.
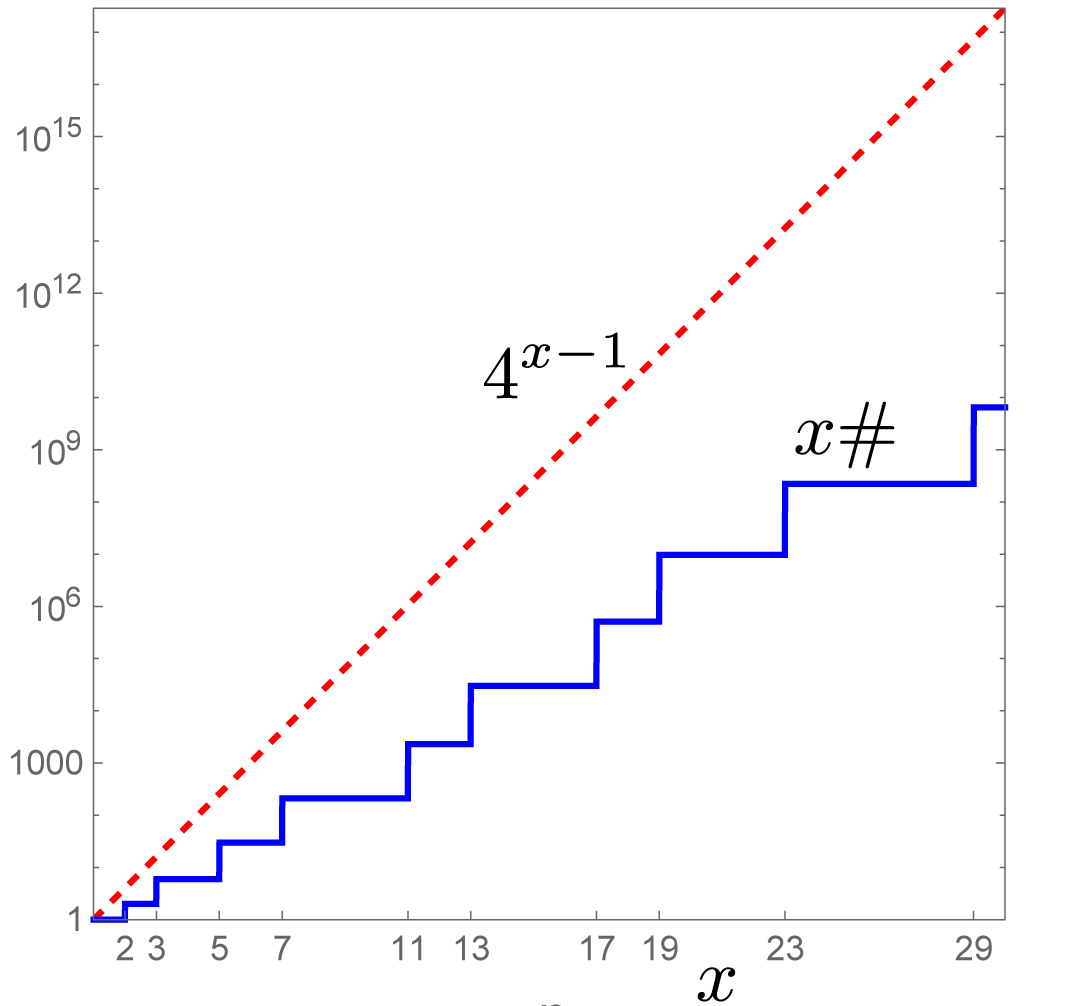
Primorial function x\# (blue) and its upper bound (red).
Central Binomial Prime Factors
Consider the one central binomial coefficient
\binom{2n}{n} = \frac{(2n)!}{n!n!} = \frac{(2n)!}{(n!)^2}.Since \lfloor n/p \rfloor factors of n! are divisible by p, and \lfloor n/p^2 \rfloor factors of n! are divisible by p^2, and so on, n! contains the prime p exactly \sum_{k\ge1} \lfloor n/p^k\rfloor times. Thus,
n!=\prod_p p^{\sum_k \lfloor n/p^k\rfloor}and
\binom{2n}{n}=\prod_p p^{\sum_k \left( \lfloor 2n/p^k\rfloor-2\lfloor n/p^k\rfloor \right) }.Since
x-1<\lfloor x \rfloor \le x,the integer summands difference
\left\lfloor \frac{2n}{p^k} \right\rfloor -2\left\lfloor \frac{n}{p^k}\right\rfloor < \frac{2n}{p^k}-2\left(\frac{n}{p^k}-1\right) = 2and thus must be either 0 or 1.
If p^k > 2n, \lfloor 2n / p^k \rfloor = 0 and \lfloor n / p^k \rfloor = 0 and no power of p divides (2n)!/(n!)^2. If p^k \le 2n, then the divisor’s highest power k \le \log 2n / \log p, but if p > \sqrt{2n}, then \log 2n / \log p < 2, and the power must be 0 or 1.
For n \ge 3, if 2n/3 < p \le n, then p \le n < 2p \le 2n < 3 p, which implies that (2n)! contains p and 2p and not 3p while n! contains p and not 2p, so the powers of p in (2n)!/(n!)^2 cancel.
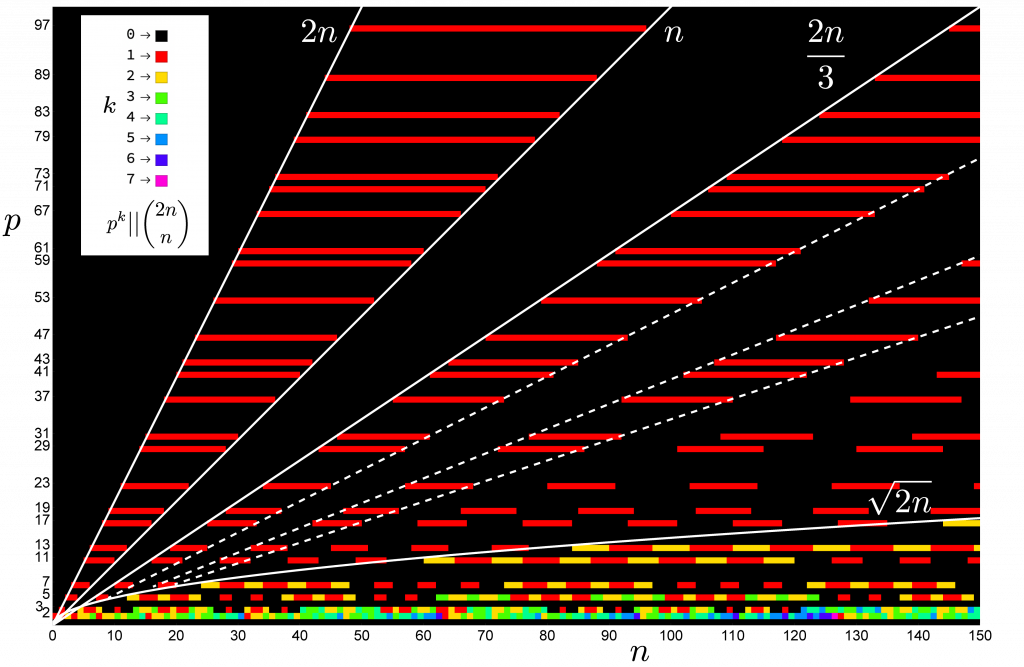
Largest prime powers dividing the central binomial coefficient. Only the “smallest” prime powers can divide the binomial multiple times.
Central Binomial Upper Bound
Split the central binomial coefficient into products of successive ranges of primes and generously bound the factors from above by the previous results to get
\binom{2n}{n}=\prod_{\smash{p}} p^{k_p} =\prod_{\smash{p \le \sqrt{2n}}} \hspace{-0.5em} p^{k_p} \prod_{\smash{\sqrt{2n} < p \le 2n/3}} \hspace{-1.5em} p^{k_p}\ \prod_{\smash{2n/3 < p \le n}} \hspace{-1.1em} p^{k_p} \prod_{\smash{n < p \le 2n}} \hspace{-0.7em}p^{k_p} \le\prod_{\smash{p \le \sqrt{2n}}} \hspace{-0.5em}2n \prod_{\smash{p \le 2n/3}} \hspace{-0.4em}p \prod_{\smash{2n/3 < p \le n}} \hspace{-0.9em}p^{0} \prod_{\smash{n < p \le 2n}} \hspace{-0.6em}p < (2n)^{\sqrt{2n}} \cdot 4^{2n/3} \cdot 1 \cdot (2n)^N,where N is the number of primes between n and 2n, if any.
Central Binomial Lower Bound
Because the central binomial coefficient is the largest,
2^{2n}=(1+1)^{2n}=\sum_{m=0}^{2n}\binom{2n}{m} = 2 + \sum_{m=1}^{2n-1}\binom{2n}{m} < 2n\binom{2n}{n},and so
\frac{4^n}{2n} < \binom{2n}{n}.Central Binomial Squeeze
Combine the central binomial coefficient upper and lower bounds to get
\frac{4^n}{2n} < \binom{2n}{n} < (2n)^{\sqrt{2n}} \cdot 4^{2n/3}(2n)^N,which simplifies to
4^{n/3} < (2n)^{\sqrt{2n}+N},and so the number of primes in n < p \le 2n is
N > \frac{2n}{3 \log_2(2n)}-\sqrt{2n}-1.Evaluate the right side to find N>1 for all n > 507. For n \le 507, the sequence of primes
2, 3, 5, 7, 13, 23, 43, 83, 163, 317, 521,where each is smaller than twice its predecessor, then suffices to prove Bertrand’s postulate for all n \ge 1.
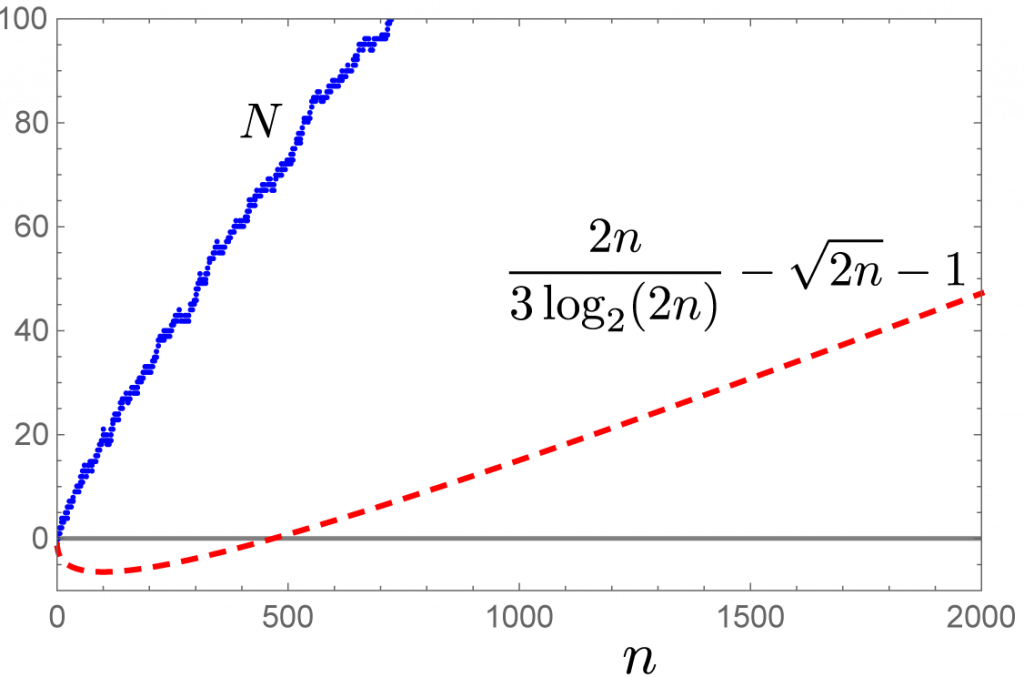
Number of primes N in n < p \le 2n (blue) and its generous lower bound (red).

Thanks, Mark! I enjoy reading your posts as well.