For the last two years, the Nonlinear Artificial Intelligence Lab and I have labored to incorporate diversity in machine learning. Diversity conveys advantages in nature, yet homogeneous neurons typically comprise the layers of artificial neural networks. In software, we constructed neural networks from neurons that learn their own activation functions (relating inputs to outputs), quickly diversify, and subsequently outperform their homogeneous counterparts on image classification and nonlinear regression tasks. Sub-networks instantiate the neurons, which meta-learn especially efficient sets of nonlinear responses.
Our examples included conventional neural networks classifying digits and forecasting a van der Pol oscillator and physics-informed Hamiltonian neural networks learning Hénon-Heiles stellar orbits.
As a final real-world example, I video recorded my wall-hanging pendulum clock, ticking beside me as I write this. Engineered to be nearly Hamiltonian, and assembled with the help of a friend, the pendulum’s Graham escapement periodically interrupts the fall of its weight as gravity compensates dissipation. Using software, we tracked the ends of its compound pendulum, and extracted its angles and angular velocities at equally spaced times. We then trained a Hamiltonian neural network to forecast its phase space orbit, as summarized by the figure below. Once again, meta-learning produced especially potent neuronal activation functions that worked best when mixed.
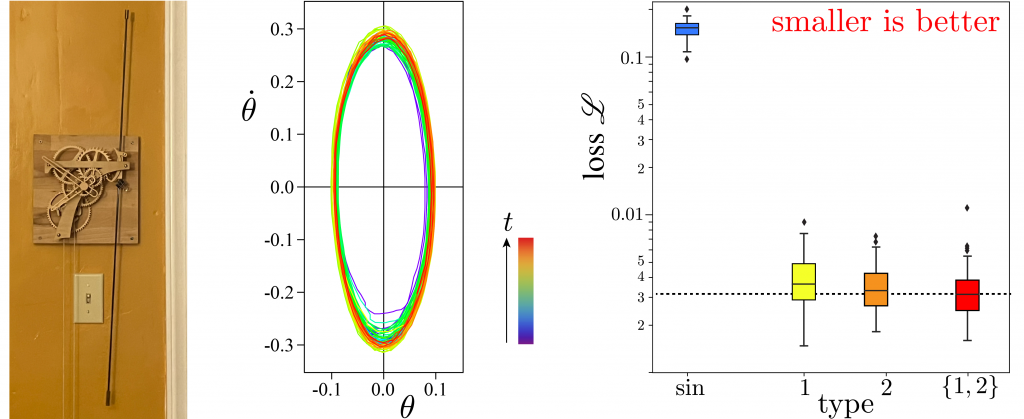
Meta-learning 2 activations for forecasting a real pendulum clock engineered to be almost Hamiltonian. Left: Falling weight (not shown) drives a wall-hanging pendulum clock. Center: State space flow from video data is nearly elliptical. Right: Box plots summarize distribution of neural network mean-square-error validation loss, starting from 50 random initializations of weights and biases, for a fully connected neural networks of sine neurons (blue), type-1 neurons (yellow), type-2 neurons (orange), and a mix of type 1 and type 2 neurons (red).

Thanks, Mark! I enjoy reading your posts as well.