Johannes Kepler asserted in 1611 that no packing of identical balls has density greater than the hexagonal close-packed “cannonball” packing of oranges at a grocery store’s fruit stand. But the gulf between intuition and proof was so large that the latter was not achieved until the work of Thomas Hales and Samuel Ferguson in 1998. And the resulting computer-assisted proof-by-exhaustion was so long and complicated that it was not finally accepted until 2017 after being formalized and certified by proof-checking computer software.
Here I present an elementary proof due to Hales of the corresponding conjecture in two dimensions, that regular hexagonal packing is the densest disk packing in the plane, as asserted by Axel Thue in 1890 and first proved by László Fejes Tóth in 1940.
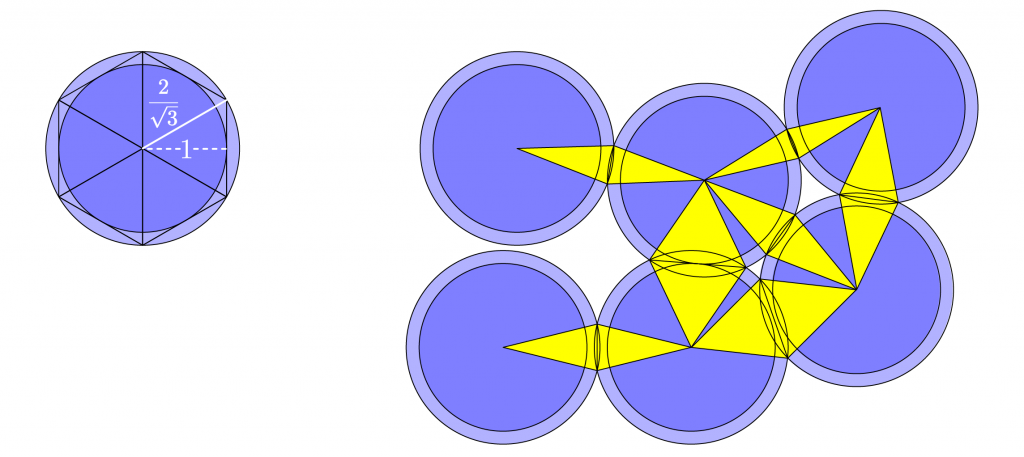
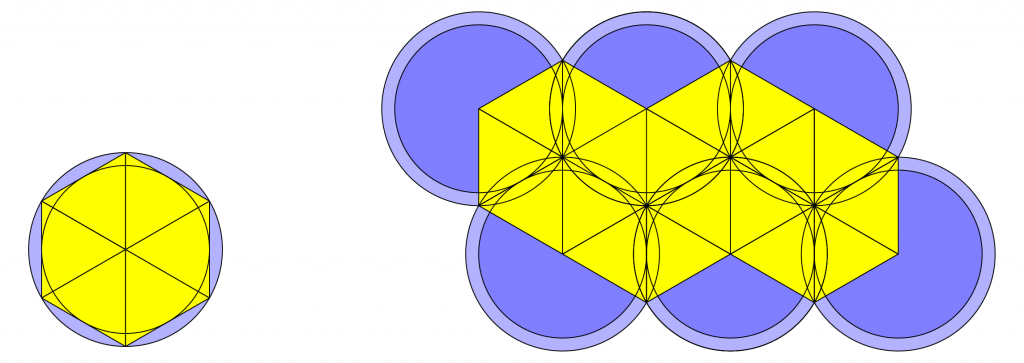
Assume the (blue) disks have radius 1, so (light blue) disks circumscribing the circumscribing hexagon have radius 2 / \sqrt{3}>1. Overlapping circumscribing disks form (yellow) triangles connecting disk centers and circumcircle intersections. Partition the plane into 3 regions: (white) background, (light and dark blue) disks sans (yellow) triangles, and (yellow) triangles.
Density of a (dark blue) disk in the circumscribing hexagon is
D_h = \frac{a_h}{A_h} = \frac{\pi 1^2}{6 \cdot (1 \cdot 2/\sqrt{3})/2} = \frac{\pi}{\sqrt{12}} \approx 0.9069.Density of a (dark blue) disk in the empty (white) background is
D_b = 0.Density of a (dark blue) disk sans (yellow) triangle, with vertex angle \theta, in (light blue) a circumscribing disk sans (yellow) triangle is
D_d = \frac{a_d}{A_d} = \frac{(2\pi-\theta)\, \pi 1^2}{(2\pi-\theta)\, \pi (2/\sqrt{3})^2} = \frac{3}{4} < D_h.Density of a (dark blue) disk in a (yellow) triangle is
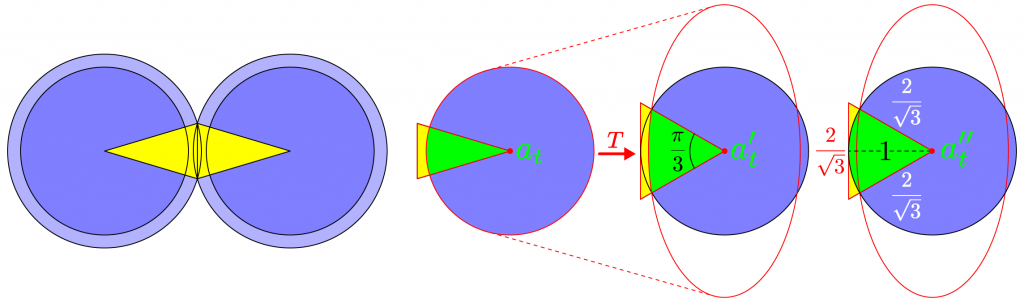
D_t = \frac{a_t}{A_t} \stackrel{T}{=} \frac{a_t^\prime}{A_t^\prime} \le \frac{a_t^{\prime\prime}}{A_t^\prime} = \frac{(1/6)\, \pi 1^2}{(1 \cdot 2/\sqrt{3})/2} = \frac{\pi}{\sqrt{12}} = D_h,where a linear transformation converts the acute (yellow) triangle to an equilateral triangle while preserving the area ratio, and the transformed (green) elliptical sector is smaller than the corresponding (green) circular sector.
Therefore, mean density of the (dark blue) disks is
D=\frac{a}{A} = \frac{A_b D_b + A_d D_d + A_t D_t}{A_b + A_d + A_t}\le\frac{A_b D_h + A_d D_h + A_t D_h}{A_b + A_d + A_t} = D_h,the hexagonal density, which is the densest possible.
