Due to the pandemic, the summer of 2019 was regrettably and unexpectedly my last Wooster summer research program, but the team was amazing. Niklas Manz and I obtained Sherman-Fairchild funding to work with Margaret McGuire ’20, Yang (Fish) Yu ’21, and Chase Fuller ’19 to computationally study reaction-diffusion phenomena. All three of their projects have now been published, with them as lead authors. Fish was lead on Disruption and Recovery, published in Physica A; Margaret was lead on Geographic Tongue, published in Chaos; and Chase was lead on Diffusion Diodes, published today in the International Journal of Unconventional Computing.
Summer 2019 Sherman-Fairchild scholars take a break in the lovely Taylor 211 computational physics lab.
With important later contributions by co-author Daniel Cohen-Cobos ’23, Chase used the Tyson-Fife model of the Belousov-Zhabotinsky reaction to numerically investigate the propagation of reaction-diffusion waves through narrow, quasi-one-dimensional channels. He created “soft” obstacles where the inhibitor’s diffusion was larger than the activator’s diffusion, so the system exhibited unidirectional or one-way propagation – a diffusion diode. Furthermore, he discovered a nonlinear compensation relationship between higher activator diffusion (causing increased wave speed) and light illumination (causing decreased wave speed) that enables normal propagation. This effect should facilitate the creation of very energy efficient on-off switches for chemical computation circuits, where small changes in light levels cause the diffusion diodes to pass or block waves.
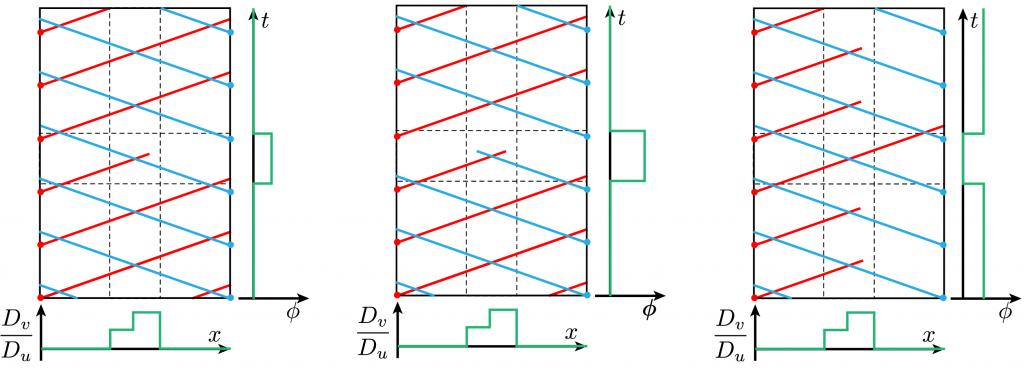
Schematic time-space plots of periodic reaction diffusion waves with variable spatial diffusion and temporal illumination illustrate light switches. Leftward (red) and rightward (blue) waves are independent experiments. Left: Faint light increase creates a diode. Middle: Strong light pulse destroys the diode and creates a 2-way barrier. Right: Faint light decrease destroys a diode and creates a 2-way opening.
