On 1852 October 23, Francis Guthrie noticed that he needed only 4 colors to color the counties of England so no two bordering counties shared the same color. This works for any map, but only in 1976, and with the aid of a computer, did Kenneth Appel and Wolfgang Haken finally prove the 4-color theorem. Here I outline an accessible proof of the simpler 5-color theorem based on Percy Heawood‘s 1890 salvage of Alfred Kempe‘s 1879 flawed proof.
Convert map to graph
Replace the map with a graph of V vertices, E edges, and F faces. Represent the 5 colors by the numbers 1, 2, 3, 4, 5.
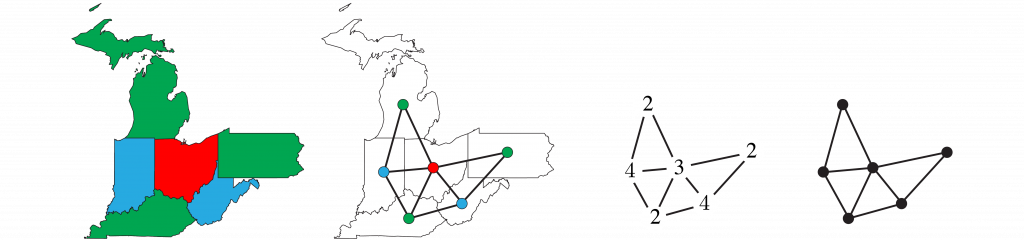
Euler characteristic
For connected planar graphs, the Euler characteristic \chi = V-E+F=2 is a topological invariant. The proof is by induction on the number of vertices. An isolated vertex V = 1 connects to no edges E = 0 but is surrounded by a single face F = 1 extending to infinity, so \chi = 1-0+1=2. Assume \chi = 2 for a graph of V vertices, and extend it in one of two ways: add an edge and a vertex, so \Delta \chi =1-1 + 0 = 0 , or add an edge connecting two existing vertices, so \Delta \chi =0-1 + 1 = 0 . Either way, the Euler characteristic is invariably \chi = 2.

Twice edges is at least thrice faces
For simple planar graphs (with no loops or repeated edges), double the number of edges is at least triple the number of faces. To prove this, first consider a maximally triangulated graph where each face (including the exterior one) is bounded by 3 edges. Tripling the faces counts each edge twice, so 2E = 3F. To reach a generic case, deleting any edge reduces this equality’s left side by 2 and reduces its right side by 3, so 2E \ge 3F.

At least one vertex has no more than 5 edges
In simple planar graphs, there exists a vertex with 5 or fewer edges. The proof is by contradiction. If each vertex connects to 6 edges, then sextupling the vertices counts each edge twice, so 2E = 6V. For the generic case, where each vertex connects to at least 6 edges, adding edges increase this equality’s left side without changing its right side, so 2E \ge 6V and E \ge 3V.

Use this inequality to eliminate vertices V from the tripled Euler characteristic 3\chi = 3V-3E+3F = 6 and get E-3E+3F\ge 6, so 3F – 6\ge 2E \ge 3F by the above twice-thrice inequality. But 3F – 6\ge 3F implies – 6\ge 0, which is a contradiction.
5-color theorem
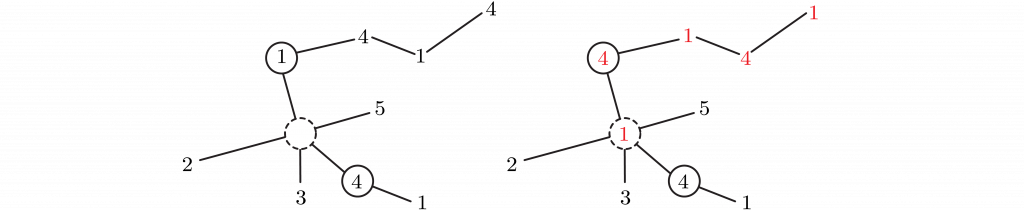
Every map is 5-colorable. The proof is by induction on the number of vertices of the corresponding graphs. A single V = 1 vertex is trivially colored by a single color. Assume all V > 1 graphs are 5-colorable and consider a V+1 graph. Delete the vertex with the fewest edges, which must be 5 or less, and the resulting graph is 5-colorable. Restore the vertex. If it is connected to 4 or less edges, color it differently than its neighbors.

If the restored vertex is connected by 5 edges, consider nonadjacent neighbor vertices V_1 and V_4 colored by colors 1 and 4. If the subgraph of vertices colored 1 and 4 is disconnected and V_1 and V_4 are in different components, interchange the 1 and 4 colors in the component including V_1 and color the restored vertex 1.
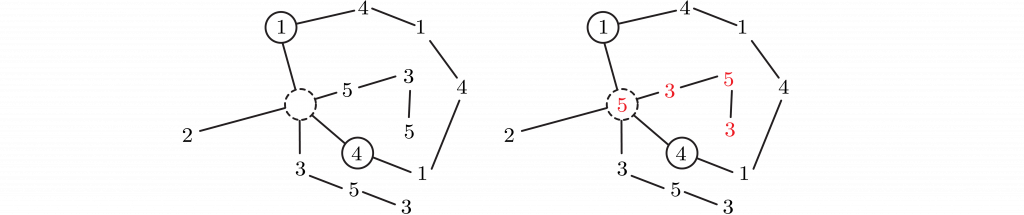
Else if V_1 and V_4 are in the same component of the subgraph, a Kempe chain barrier separates the subgraph connecting V_3 and V_5, so interchange the 3 and 5 colors in one component and color the restored vertex 5.

Thanks, Mark! I enjoy reading your posts as well.