Long before he won the Nobel Prize in Physics, and while still a Wooster undergraduate, Arthur Compton realized a third way to demonstrate Earth’s spin (after pendulums and gyroscopes).
Compton reported his results in a manuscript submitted to the journal Science on 1913 January 13 and published as “A Laboratory Method of Demonstrating the Earth’s Rotation”, Arthur Holly Compton, Physical Laboratory, University of Wooster, Science, 1913 May 23, volume 37, issue 960, pages 803-806.
Compton’s generator is nowadays often used as a text book example of the \vec F_C = 2 m\, \vec v \times \vec \omega Coriolis pseudo-force deflecting the fluid in a circular tube as it is flipped in Earth’s rotating reference frame, which is analogous to the \vec F_B = q\, \vec v \times \vec B magnetic force deflecting a moving charge. However, an inertial perspective is simpler. After viscosity has damped the fluid motion relative to Earth, the fluid farther from the rotation axis is moving faster relative to distant stars, so quickly flipping the ring reverses the speed gradient and induces transient circulation.
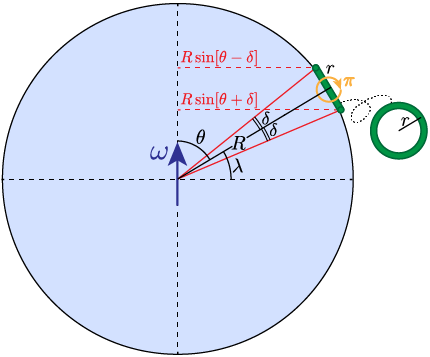
Flipping Compton’s ring π = 180° causes the stationary fluid inside to circulate, generating motion and revealing Earth’s spin.
Flipping a wire loop in a magnetic field generates transient electric current like flipping Compton’s ring in a spinning reference frame generates transient fluid flow, where the magnetic field plays the role of the angular velocity; indeed, the former is an electric generator and the latter is a motion generator!
As in the above figure, assume Earth has radius R and angular speed \omega. Assume the ring is at co-latitude \theta and subtends an angle 2\delta from Earth’s center. Then the spread in the fluid’s inertial speeds is
\delta v = \omega R \sin[ \theta + \delta] – \omega R \sin[\theta – \delta] = 2\omega R \cos \theta\sin \delta.If the ring’s radius r \ll R , then
1 \gg r / R \approx \delta \approx \sin\delta,and so
\delta v = 2 \omega r \cos \theta = 2 \omega r \sin \lambda,where \lambda is the latitude. As checks, \delta v = 0 when \lambda = 0 (straddling the equator), and \delta v = 2\omega r when \lambda = \pi/2 (straddling the north pole).
For Earth’s \omega = 2\pi/\text{day} angular speed, flipping a quiescent r = 1~\text{m} ring at \lambda = \pi/4 mid latitude generates an initial fluid speed \delta v = 0.1~\text{mm/s}. Compton amplified this motion by using a microscope to view the fluid through a window in a constriction of the tube.

Thanks, Mark! I enjoy reading your posts as well.