Slide rules were the analog computers that ruled science and engineering for 400 years. Their brilliant innovation was using logarithms to convert multiplication and division to addition and subtraction,
\log xy = \log x + \log yand
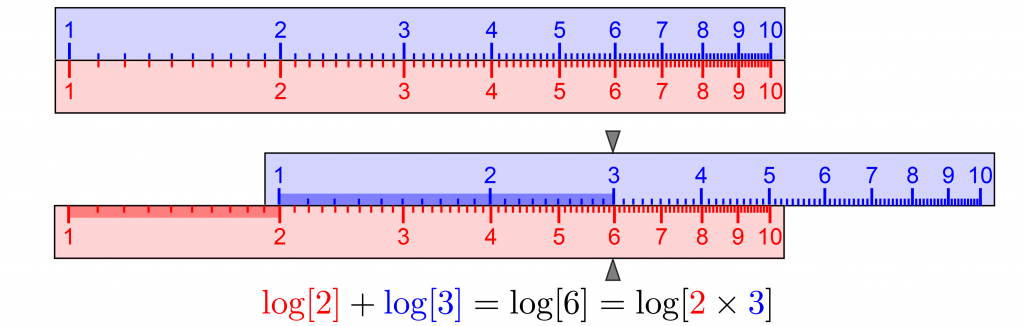
\log \frac{x}{y} = \log x - \log y.Slide rules feature logarithmic scales that slide past each other. For straight slide rules, logarithms of the numbers are proportional to their distances along them. To multiply 2\times 3 = 6, as below, slide the upper (blue) scale from 1 to 2 along the lower (red) scale, add the distance from 1 to 3 along the upper (blue) scale, and read the product from the lower (red) scale.
Logarithms of the numbers are proportional to their distances along the straight slide rule scales. Slide the upper (blue) scale to multiply numbers by adding these distances.
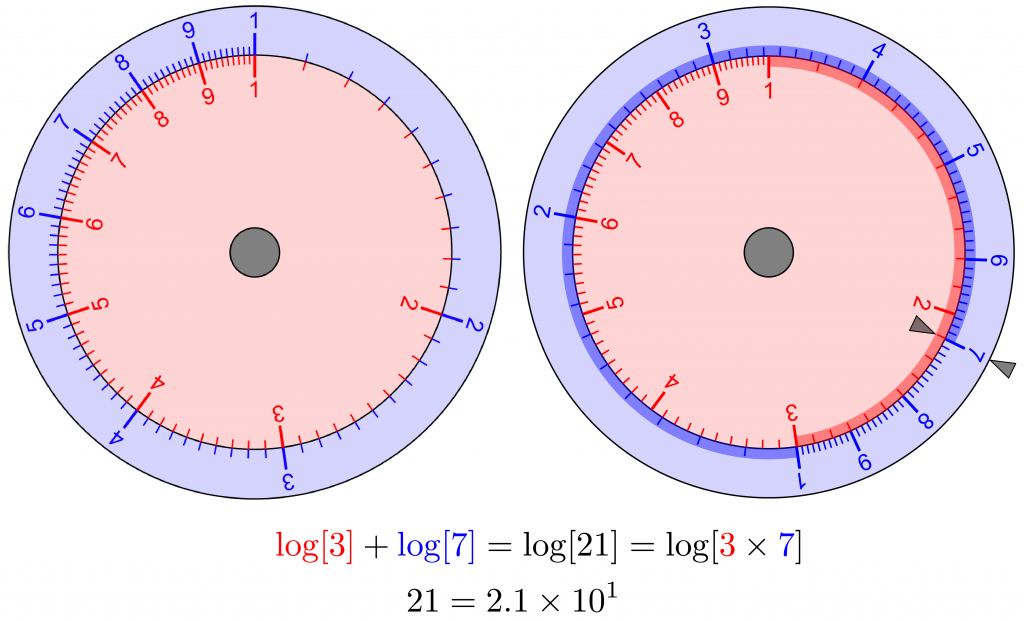
For circular slide rules, logarithms of the numbers are proportional to their distances around them. To multiply 3\times 7 = 21, as below, rotate the outer (blue) scale from 1 to 3 around the inner (red) scale, add the distance from 1 to 7 around the outer (blue) scale, and read the product from the inner (red) scale. Circular slide rules eliminate off-scale calculations because they naturally wrap around, with each wrap multiplying (or dividing) the numbers by 10.
Logarithms of the numbers are proportional to their distances around the circular slide rule scales. Rotate the outer (blue) scale to multiply numbers by adding these distances.
