A complex function that is its own derivative normalized to one at zero implicitly defines the famous Archimedean and Euler constants of circular motion and exponential growth. Even in a world of strong gravity, where the ratio of a circle’s circumference to its diameter noticeably varied from place to place, this exponential function and the axioms of mathematics would generate these same transcendental numbers.
Assuming the Taylor series expansion
f(z) = \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!} z^n,where z = x + i y \in \mathbb{C} with x,y \in \mathbb{R} and i = \sqrt{-1}, the derivative condition
f^\prime(z) = f^{(1)}(z) = \sum_{n=1}^\infty \frac{f^{(n)}(0)}{(n-1)!} z^{n-1} = \sum_{n=0}^\infty \frac{f^{(n+1)}(0)}{n!} z^n \equiv f(z) = f^{(0)}(z)coupled with the normalization condition
f^{(n+1)}(0) = f^{(n)}(0) = f^{(n-1)}(0) = \cdots = f^{(1)}(0) =f^{(0)}(0) = f(0) \equiv 1implies
f(z) = \sum_{n=0}^\infty \frac{z^n}{n!} \equiv \exp z.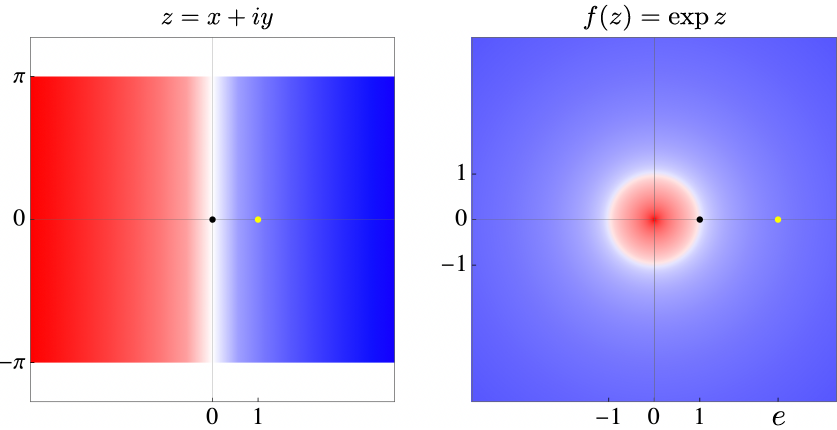
Complex exponential repeatedly maps horizontal strips (left) to the entire complex plane (right), thereby defining the Archimedes and Euler constants. Click for a better view.
Numerically plot this expression to discover two jewels. As in the figure, the exponential function maps the imaginary axis to the unit circle f(i\mathbb{R}) \rightarrow \mathbb{S}, with negative real parts forcing complex numbers inside (red) and positive real parts forcing complex numbers outside (blue). The function is exponential on the real axis with e-folding time 1, so f(1)=e, but periodic on the imaginary axis with period \tau, so f(z+i\tau)=f(z). Specifically, as it maps 1 to e, it maps horizontal strips of height \tau = 2\pi onto the entire complex plane, where
\pi =3.14159265358979323846264338327950\ldotsand
e = 2.71828182845904523536028747135266\ldotsare associated with Archimedes and Euler.
