In quantum electrodynamics, the bare charge of an electron is infinite, but the renormalized dressed charge is finite. The bare electron shields itself by polarizing the virtual electron-positron pairs of the nearby quantum vacuum to reduce its coupling at large distances to
∞ – ∞ = I 1 137 \infty – \infty \stackrel{I}{=} \sqrt{\frac{1}{137}} ∞ – ∞ = I 1 3 7 1 in natural units, where the “I” decorating the equals sign denotes an informal relationship. Renormalization techniques help physicists make sense of divergent sums and integrals used to calculate quantities like running coupling “constants” that vary with interaction energy and set the strengths of the fundamental forces.
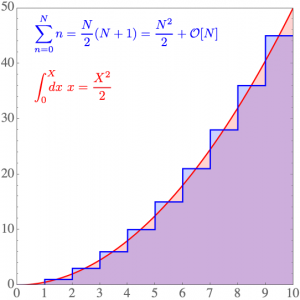
Corresponding sum and integral diverge together For a simple example, the sum of natural numbers
∑ n = 0 N n = 1 + 2 + 3 + ⋯ + N = N 2 ( N + 1 ) \sum_{n=0}^N n = 1+2+3+\cdots+N= \frac{N}{2}(N+1) n = 0 ∑ N n = 1 + 2 + 3 + ⋯ + N = 2 N ( N + 1 ) diverges as N → ∞ N\rightarrow \infty N → ∞ integral of positive real numbers
∫ 0 X d x x = X 2 2 \int_{0}^X \hspace{-0.8em}dx\ x =\frac{X^2}{2} ∫ 0 X d x x = 2 X 2 diverges as X → ∞ X\rightarrow \infty X → ∞ convergence factor and formally subtract the integral from the sum
∑ n = 0 ∞ n − ∫ 0 ∞ d x x = lim λ → 0 ( ∑ n = 0 ∞ n e − λ n − ∫ 0 ∞ d x x e − λ x ) = lim λ → 0 ( S − I ) . \sum_{n=0}^\infty n -\int_{0}^\infty \hspace{-0.8em} dx\, x =\color{red}\lim_{\lambda \rightarrow 0}\color{black}\left( \sum_{n=0}^\infty n\, \color{red}e^{-\lambda n}\color{black}-\int_{0}^\infty \hspace{-0.8em} dx\, x\, \color{red}e^{-\lambda x} \color{black}\right)=\color{red}\lim_{\lambda \rightarrow 0}\color{black}\left(\mathcal{S}-\mathcal{I}\right). n = 0 ∑ ∞ n − ∫ 0 ∞ d x x = λ → 0 l i m ( n = 0 ∑ ∞ n e − λ n − ∫ 0 ∞ d x x e − λ x ) = λ → 0 l i m ( S − I ) . To evaluate the cancellation, integrate the integral with respect to the convergence parameter λ > 0 \lambda>0 λ > 0
I = ∫ 0 ∞ d x x e − λ x = − d d λ ∫ 0 ∞ d x e − λ x = − d d λ ( e − λ x − λ ) ∣ 0 ∞ = − d d λ ( 1 λ ) = 1 λ 2 . \mathcal{I}=\int_{0}^\infty \hspace{-0.8em}dx\ x\, \color{red}e^{-\lambda x}\color{black} =-\frac{d}{d\lambda}\int_{0}^\infty \hspace{-0.8em}dx\ e^{-\lambda x} =-\frac{d}{d\lambda}\left(\frac{e^{-\lambda x}}{-\lambda}\right)\bigg|_{0}^\infty=-\frac{d}{d\lambda}\left(\frac{1}{\lambda}\right)=\frac{1}{\lambda^2}. I = ∫ 0 ∞ d x x e − λ x = − d λ d ∫ 0 ∞ d x e − λ x = − d λ d ( − λ e − λ x ) ∣ ∣ ∣ ∣ ∣ 0 ∞ = − d λ d ( λ 1 ) = λ 2 1 . Next integrate the sum with respect to λ \lambda λ
S = ∑ n = 0 ∞ n e − λ n = − d d λ ∑ n = 0 ∞ e − λ n = − d d λ ∑ n = 0 ∞ ( e − λ ) n \mathcal{S}=\sum_{n=0}^\infty n\,\color{red} e^{-\lambda n}\color{black} = -\frac{d}{d\lambda} \sum_{n=0}^\infty e^{-\lambda n} = -\frac{d}{d\lambda} \sum_{n=0}^\infty \left(e^{-\lambda}\right)^n S = n = 0 ∑ ∞ n e − λ n = − d λ d n = 0 ∑ ∞ e − λ n = − d λ d n = 0 ∑ ∞ ( e − λ ) n and sum the resulting geometric series to find
S = − d d λ ( 1 1 − e − λ ) = e − λ ( 1 − e − λ ) 2 e 2 λ e 2 λ = e λ ( e λ − 1 ) 2 = e λ ( 1 − e λ ) 2 , \mathcal{S}= -\frac{d}{d\lambda} \left( \frac{1}{1-e^{-\lambda}} \right)= \frac{e^{-\lambda}}{\left(1-e^{-\lambda}\right)^2}\color{red}\frac{e^{2\lambda}} {e^{2\lambda}}\color{black}= \frac{e^{\lambda}}{\left(e^{\lambda}-1\right)^2}\color{red}= \frac{e^{\lambda}}{\left(1-e^{\lambda}\right)^2}\color{black}, S = − d λ d ( 1 − e − λ 1 ) = ( 1 − e − λ ) 2 e − λ e 2 λ e 2 λ = ( e λ − 1 ) 2 e λ = ( 1 − e λ ) 2 e λ , which is thus an even function of λ \lambda λ
S = 1 + λ + λ 2 / 2 ! + λ 3 / 3 ! + ⋯ ( 1 + λ + λ 2 / 2 ! + λ 3 / 3 ! + ⋯ – 1 ) 2 = 1 + λ + λ 2 / 2 + ⋯ λ 2 ( 1 + λ / 2 + λ 2 / 6 + ⋯ ) 2 , \mathcal{S}=\frac{1+\lambda+\lambda^2/2!+\lambda^3/3!+\cdots}{\left(1+\lambda+\lambda^2/2!+\lambda^3/3!+\cdots – 1 \right)^2}=\frac{1+\lambda+\lambda^2/2+\cdots}{\lambda^2\left(1+\lambda/2+\lambda^2/6+\cdots \right)^2}, S = ( 1 + λ + λ 2 / 2 ! + λ 3 / 3 ! + ⋯ – 1 ) 2 1 + λ + λ 2 / 2 ! + λ 3 / 3 ! + ⋯ = λ 2 ( 1 + λ / 2 + λ 2 / 6 + ⋯ ) 2 1 + λ + λ 2 / 2 + ⋯ , expand the denominator square
( 1 + λ / 2 + λ 2 / 6 + ⋯ ) 2 = + 1 + λ / 2 + λ 2 / 6 + ⋯ + λ / 2 + λ 2 / 4 + λ 3 / 12 + ⋯ + λ 2 / 6 + λ 3 / 12 + λ 4 / 36 + ⋯ = 1 + λ + 7 λ 2 / 12 + ⋯ \begin{array}{ccc}\left(1+\lambda/2+\lambda^2/6+\cdots\right)^2=&+1\hspace{1.2em}+\lambda/2\hspace{0.7em}+\lambda^2/6\hspace{0.2em}\phantom{+\cdots}\\ \rule{0pt}{1.3em}&+\lambda/2\hspace{0.43em}+\lambda^2/4\hspace{0.37em}\color{red}+\lambda^3/12\color{black}\phantom{+\cdots}\\ \rule{0pt}{1.3em}&+\lambda^2/6\color{red}+\lambda^3/12+\lambda^4/36+\cdots&\color{black} = 1+\lambda+7\lambda^2/12+\cdots\end{array} ( 1 + λ / 2 + λ 2 / 6 + ⋯ ) 2 = + 1 + λ / 2 + λ 2 / 6 + ⋯ + λ / 2 + λ 2 / 4 + λ 3 / 1 2 + ⋯ + λ 2 / 6 + λ 3 / 1 2 + λ 4 / 3 6 + ⋯ = 1 + λ + 7 λ 2 / 1 2 + ⋯ and use long division
1 − λ 2 / 12 + ⋯ 1 + λ + 7 λ 2 / 12 + ⋯ ) 1 + λ + 9 λ 2 / 2 9 + ⋯ ‾ 1 + λ + 7 λ 2 / 12 + ⋯ ‾ 0 − λ 2 / 12 + ⋯ − λ 2 / 12 + ⋯ ‾ 0 + ⋯ \begin{array}{r}1-\lambda^2/12+\cdots\\ 1+\lambda+7\lambda^2/12+\cdots \,{\overline{\smash{\big)}\,1+\lambda+\phantom{9}\lambda^2/2\phantom{9} +\cdots}}\\ \underline{1+\lambda+7\lambda^2/12+\cdots }\\0-\lambda^2/12+\cdots\\ \underline{-\lambda^2/12+\cdots}\\0+\cdots \end{array} 1 − λ 2 / 1 2 + ⋯ 1 + λ + 7 λ 2 / 1 2 + ⋯ ) 1 + λ + 9 λ 2 / 2 9 + ⋯ 1 + λ + 7 λ 2 / 1 2 + ⋯ 0 − λ 2 / 1 2 + ⋯ − λ 2 / 1 2 + ⋯ 0 + ⋯ to show
S = 1 λ 2 ( 1 − λ 2 12 + O [ λ 4 ] ) = 1 λ 2 − 1 12 + O [ λ 2 ] . \mathcal{S} = \frac{1}{\lambda^2} \left(1-\frac{\lambda^2}{12}+\mathcal{O}[\lambda^4]\right) =\frac{1}{\lambda^2}-\frac{1}{12}+\mathcal{O}[\lambda^2]. S = λ 2 1 ( 1 − 1 2 λ 2 + O [ λ 4 ] ) = λ 2 1 − 1 2 1 + O [ λ 2 ] . For finite λ \lambda λ
S − I = ∑ n = 0 ∞ n e − λ n − ∫ 0 ∞ d x x e − λ x = 1 λ 2 − 1 12 + O [ λ 2 ] − 1 λ 2 = − 1 12 + O [ λ 2 ] , \mathcal{S}-\mathcal{I}=\sum_{n=0}^\infty n\, e^{-\lambda n}-\int_{0}^\infty \hspace{-0.8em} dx\, x\,e^{-\lambda x} = \frac{1}{\lambda^2}-\frac{1}{12}+\mathcal{O}[\lambda^2]-\frac{1}{\lambda^2}= -\frac{1}{12}+\mathcal{O}[\lambda^2], S − I = n = 0 ∑ ∞ n e − λ n − ∫ 0 ∞ d x x e − λ x = λ 2 1 − 1 2 1 + O [ λ 2 ] − λ 2 1 = − 1 2 1 + O [ λ 2 ] , and for vanishing λ \lambda λ
lim λ → 0 ( ∑ n = 0 ∞ n e − λ n − ∫ 0 ∞ d x x e − λ x ) = − 1 12 . \color{red}\lim_{\lambda \rightarrow 0}\color{black}\left( \sum_{n=0}^\infty n\, \color{red}e^{-\lambda n}\color{black}-\int_{0}^\infty \hspace{-0.8em} dx\, x\, \color{red}e^{-\lambda x} \color{black}\right) = -\frac{1}{12}. λ → 0 l i m ( n = 0 ∑ ∞ n e − λ n − ∫ 0 ∞ d x x e − λ x ) = − 1 2 1 . Thus, removing nonphysical infinity in a controlled way exposes a finite component
∞ – ∞ = I − 1 12 \infty – \infty \stackrel{I}{=} -\frac{1}{12} ∞ – ∞ = I − 1 2 1 of the divergent natural numbers sum. To celebrate this hidden “golden nugget”, write
1 + 2 + 3 + ⋯ = R − 1 12 , 1+2+3+\cdots \stackrel{R}{=} -\frac{1}{12}, 1 + 2 + 3 + ⋯ = R − 1 2 1 , where”R” denotes regularized , renormalized , and remainder . “R” also denotes Ramanujan , who discovered this association without any formal mathematical training, and Riemann , whose famous zeta function ζ [ s ] \zeta[s] ζ [ s ]
In brief, use the convergence factor to tame infinity by isolating the diverging, remaining, and vanishing parts of the natural numbers sum
∑ n = 1 ∞ n = λ ↓ 0 ∑ n = 0 ∞ n e − λ n = λ ↓ 0 + 1 λ 2 ⏟ Diverge − 1 λ 2 12 ⏟ Remain − 1 λ 2 12 + O [ λ 2 ] ⏟ Vanish = R − 1 12 . \sum_{n=1}^\infty n\stackrel{\color{red}\lambda \downarrow 0}{=}\color{black}\sum_{n=0}^\infty n\color{red}\, e^{-\lambda n}\color{black}\stackrel{\color{red}\lambda \downarrow 0}{=}\color{red}\underbrace{\ +\frac{1}{\lambda^2}\ \ }_\text{Diverge}\color{black}\underbrace{\ -\frac{1\vphantom{\lambda^2}}{12}\ \ }_\text{Remain}\color{red} \underbrace{\vphantom{-\frac{1\vphantom{\lambda^2}}{12}}+\mathcal{O}[\lambda^2]}_\text{Vanish}\color{black}\ \stackrel{R}{=}-\frac{1}{12}. n = 1 ∑ ∞ n = λ ↓ 0 n = 0 ∑ ∞ n e − λ n = λ ↓ 0 Diverge + λ 2 1 Remain − 1 2 1 λ 2 Vanish − 1 2 1 λ 2 + O [ λ 2 ] = R − 1 2 1 . Discard the first, retain the second, and let go the third.
Thanks, Mark! I enjoy reading your posts as well.